1. 卷积
卷积是通过两个函数生成第三个函数的一种数学算子:
\begin{equation}
y(\color{red}{t})= \int_{-\infty}^{\infty} x(\tau) h(t-\tau) d\color{blue}{\tau}
\end{equation}
我们先什么都不要管,只需要注意,不要把公式中的 $\color{red}{t}$ 和 $\color{blue}{\tau}$ 混淆了。
2. 卷积的解释
贴近生活的解释永远比公式更好理解,参考网上卷积的各种血腥残暴的解释。这里,我们使用一个温和的例子。
假设你是一名研究生,你还有三天的时间来完成老板的任务,由于患有拖延症,你工作的热情可如下图表示: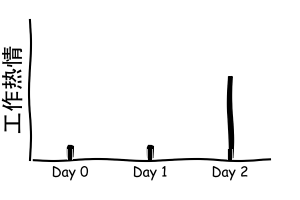
上面就是你的输入函数 $x(t)$,具体内容为:
\begin{equation*}
x(0) = 0.1, \quad
x(1) = 0.1, \quad
x(2) = 0.6.
\end{equation*}
按照你这个效率,完全不可能完成任务,因此老板会每天苦口婆心的来 push 你。老板的 push 就是 $h(t)$ 函数,我们称之为响应函数。基本上,随着时间的流逝,老板的劝说只是浪费了一点口水,对你的作用越来越小。所以,我们的 $h(t)$ 函数应该长这样:
$h(t)$ 的具体内容为:
\begin{equation*}
h(0) = 8, \quad
h(1) = 3, \quad
h(2) = 2.
\end{equation*}
意思就是老板当天的劝说对你的作用是8倍,过了一天后为3倍,过了两天后为2倍。也就是说,$h$ 函数作用于工作热情上的效果是这样的:对当天工作热情的效果是 8 倍,对昨天工作热情的效果是 3 倍,对前天工作热情的效果是 2 倍。其他时候我们记为 $h^{+}=0$
那在老板的 push 下,我们的工作热情是怎么样的呢?
这里就是输入函数在响应的作用下,得到输出函数的问题,也就是求卷积。说了这么多,好像只是介绍了我们的 $x$ 和 $h$ 函数,卷积到底是什么意思呢?让我们看一下 $x$ 和 $h$ 的卷积会发生什么。
Day 0:今天不太想工作,只有 0.1 的意愿,但是老板来 push 了,最终的工作意愿为:
\begin{equation*}
\begin{split}
y(0) &= \int_0^2 x(\tau)h(0-\tau)d\tau \\
&= \color{red}{x(0)}h(0) + \color{blue}{x(1)}h^+ +\color{blue}{x(2)}h^+ \\
&= \color{red}{x(0)}h(0) =0.8
\end{split}
\end{equation*}
该公式的意思可以这样理解:将 $h$ 函数作用在输入上,得到了我们的输出。根据 $h$ 函数的特性,它只作用在今天、昨天和前天的数据上 (以 $y(0)$ 中的 $0$ 为参考),对于明天 ($x(1)$) 和后天的数据 ($x(2)$) 的数据没有作用。Day 1: 昨天老板骂了一顿,今天又来了,老板昨天的效果也还在。最终,我们的工作热情为:
\begin{equation*}
\begin{split}
y(1) &= \color{blue}{x(0)}h(1)+\color{red}{x(1)}h(0)+\color{blue}{x(2)}h^+ \\
&= 0.8+0.3=1.1
\end{split}
\end{equation*}
意思就是今天你的工作热情只有 0.1,老板把你骂了后,你的热情变成了0.8;除此之外,老板昨天劝说的效果还在,只是从 8 倍的作用变成了 3 倍。按照 $h$ 函数的作用,将所有输入结果叠加。Day 2:同样的:
\begin{equation*}
\begin{split}
y(2) &= \color{blue}{x(0)}h(2)+\color{blue}{x(1)}h(1)+\color{red}{x(2)}h(0) \\
&=4.8+0.3+0.2=5.3
\end{split}
\end{equation*}
我们可以把 $h$ 看做权,这个计算实际上就相当于对 $x$ 进行了加权叠加。Day 3: 虽然从今天开始我们不再有新的工作热情(输入数据),但是思想教育的效果依然余留,工作效率在老板 push 的作用下为:
\begin{equation*}
\begin{split}
y(3) &= \color{blue}{x(0)}h^++\color{blue}{x(1)}h(2)+\color{blue}{x(2)}h(1) \\
&=1.8 + 0.2 = 2
\end{split}
\end{equation*}
幸好,根据 $h$ 的加权作用,老板第一天的教育终于被你忘了。Day 4: 快要迎来美好时光,老板前几天的教育都要被你忘了。
\begin{equation*}
\begin{split}
y(3) &= \color{blue}{x(0)}h^++\color{blue}{x(1)}h^++\color{blue}{x(2)}h(2) \\
&=1.2
\end{split}
\end{equation*}
老板的督促使得你保持了几天工作热情。根据你三分钟热度的性格,今天之后,又过上了毫无工作热情的生活。
我们复习一下卷积的公式:
\begin{equation}
y(\color{red}{t})= \int_{-\infty}^{\infty} x(\tau) h(t-\tau) d\color{blue}{\tau}
\end{equation}
从上面的例子可以看出,卷积就是对于每一个位置 $t_i \in (-\infty,\infty)$,将输入 $x$ (整个输入,上面几式中颜色标注),按照 $h$ 的方式加权叠加起来,这里 $h$ 的方式就是以当前时间为基准 ($t_i$,红色标注),对当天的效应是 8,昨天的效应是 3,前天的效应是 2。
最后,给出在老板的连番督促下,你的工作热情: