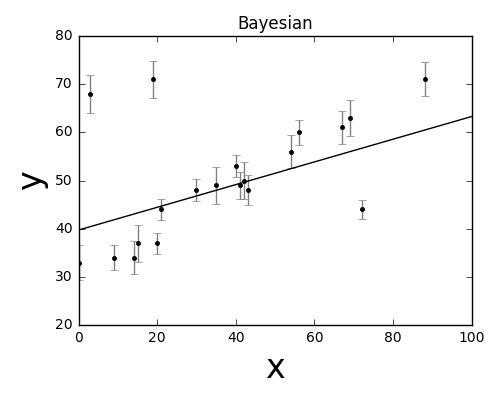
1. 频率主义与贝叶斯主义
频率主义认为概率与事件的频率有关,贝叶斯主义认为概率是对事件的认知程度的度量。举个例子说明一下,假设我们多次测量了一个棍子的长度,得到的观测数据为: Data = [L1, L2],其中 L1 占比 30%,L2 占比 70%(假设测量结果就两种情况)。
频率主义认为:棍子的长度 (length) 是固定值,即参数是固定的。由于测量误差的存在,测量结果
L1发生的频率为 30%,L2发生的频率为 70%。根据频率主义者对概率的认知,可用如下公式表示:\begin{equation*}
P(Data=L1 \mid length)= 30\% \\
P(Data=L2 \mid length)= 70\%
\end{equation*}
其意义为:在 length 的条件下(在棍子长度为固定某值得条件下),得到L1的概率为 30%,得到L2的概率为 70%。贝叶斯主义认为:观测结果 (Data) 是固定的,是我们对事件的认知。根据观测结果,棍子长度为
L1的概率为 30%,为L2的概率为7 0%,即参数 (length) 不是固定的,而是一个分布。概率就是我们对棍子长度的认知程度,我们 30% 地认为棍子长度为L1, 70% 地认为棍子长度为L2,可用如下公式表示:
\begin{equation*}
P(length=L1 \mid Data)= 30\% \\
P(length=L2 \mid Data)= 70\%
\end{equation*}
其意思为:在观测数据 (Data) 的条件下,棍子长度为L1的概率为 30%,为L2的概率为 70%。
为了更直观的说明频率主义和贝叶斯主义,根据上述例子,有如下图像。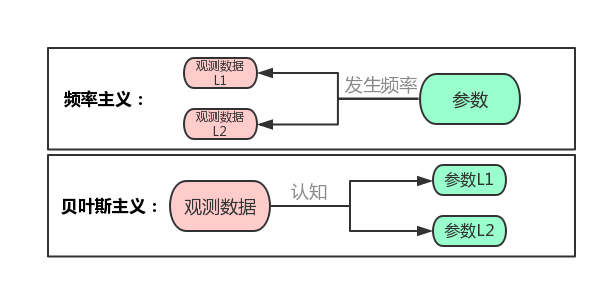
$\quad$
2. 频率主义参数估计
我们用线性拟合作为例子,考虑下面的数据集合 x、y和y 的误差 e,数据来源于Frequentism and Bayesianism II: When Results Differ。
先看一下数据长什么样。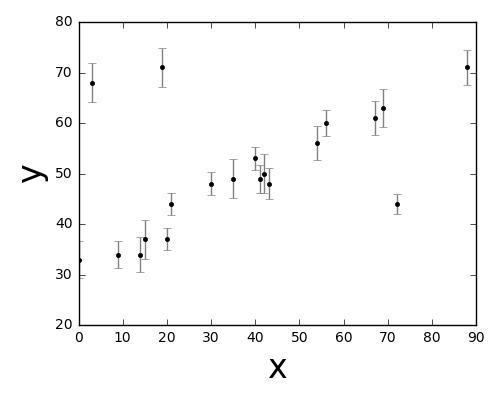
我们的任务是找出一条直线来拟合数据,这里我们采用最大似然估计法(常用的最小二乘估计为最大似然估计的一种特例:正态最大似然估计)。
我们构造一个线性模型,参数有斜率和截距,模型定义如下:
\begin{equation}
\label{model}
\hat{y} = a_0x+a_1
\end{equation}
根据观测数据 x,y 集合,估计 $a=(a_0,a_1)$。
对于某一次测量值 ($d_i=(x_i,y_i,e_i)$),假设测量误差按正态分布,该事件发生的概率分布满足:
\begin{equation}
\label{pro}
P(d_i \mid a) = \frac{1}{\sqrt{2\pi e_i^2}}exp[-\frac{(y_i-\hat{y}_i)^2}{2e_i^2}]
\end{equation}
似然函数为每个观测值概率的乘积:
\begin{equation}
\label{like}
\ell (d \mid a) = \prod_{i=1}^N P(d_i \mid a)
\end{equation}
最大似然法就是使似然函数最大,这里很好理解。还是使用上面棍子的例子,假设我们测得的数据为 (10.1 米, 9.9 米),根据测量数据我们估计棍子到底多长。那怎么估计呢?考虑这样的一个问题:棍子长度为多少时,我们最大概率上得到的测量数据为 (10.1 米, 9.9 米),答案呼之欲出,我们猜测棍子的长度为 10.0 米,因为这样我们最大概率获得了我们的观测数据。如果棍子长度为 1 米,我们基本上不可能得到(10.1 米, 9.9 米)这样的观测数据。也就是说,我们需要求一个 length,使得 $P(10.1 \mid length)\cdot P(9.9 \mid length)$ 最大,也就是最大似然法。
回到上面的线性拟合问题,我们需要估计参数 $a$,使得 $d$ 发生的概率最大。一般情况下,因为似然估计值可能非常小,通常更方便的做法是取似然函数的对数,将公式 (\ref{pro}) 代入公式 (\ref{like}) 并取对数:
\begin{equation}
\begin{split}
log \ell (d \mid a) = -\frac{1}{2}\sum_{i=1}^N[log(2\pi e_i^2)+ \frac{(y_i-\hat{y}_i)^2}{e_i^2}]
\end{split}
\end{equation}
\begin{equation}
log \ell (d \mid a) = const - \sum_{i=1}^N\frac{1}{2e_i^2}(y_i-\hat{y}_i^2)
\end{equation}
我们需要求解 $a$ 使得上式最大化,等价于最小化下式:
\begin{equation}
loss = \sum_{i=1}^N\frac{1}{2e_i^2}(y_i-\hat{y})
\label{loss}
\end{equation}
上式与我们的直觉很符合,为了找到一个最佳拟合直线,我们需要观测值与模型值的差的平方和最小,这也就是最小二乘方法,或者说最小平方损失。
公式 (\ref{loss}) 的解算方法很多,这里用矩阵的解算方法。记误差 $e^2$ 组成的矩阵为 $P$,$v= y_i-\hat{y}$ 组成的矩阵为 $V$,公式 (\ref{loss}) 最小化等价于:
\begin{equation}
V^T P V = min
\label{vpv}
\end{equation}
将 $v= y_i-\hat{y}$ 写成矩阵形式:
\begin{equation}
V = Ba -l
\end{equation}
其中,$a=[a_0, a_1]$,$l=[-y]$,$B=[-x, -1]$。
求解公式 (\ref{vpv}):
\begin{equation}
\begin{split}
&\frac{\partial{V^TPV}}{\partial a}=2V^T P \frac{\partial V}{\partial{a}}= V^TPB=0 \\
&\Rightarrow B^TPV=0 \\
&\Rightarrow B^TP(Ba-l)=0 \\
&\Rightarrow a = (B^TPB)^{-1}B^TPl
\end{split}
\end{equation}
根据上式,即可利用频率主义的方法估计参数 $a$。所得结果如下图所示: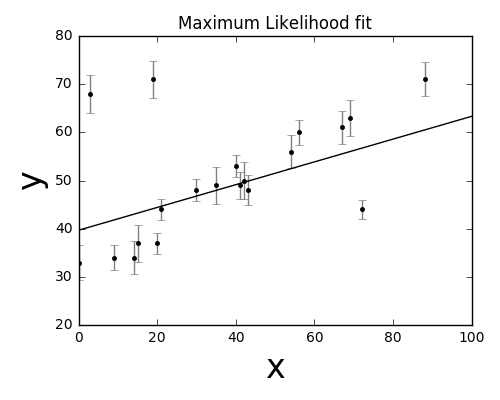
总结:频率主义认为参数是固定的(斜率和截距),利用最大似然法估计参数,使得在此参数条件下,得到该组观测数据的概率最大。
3. 贝叶斯主义参数估计
贝叶斯主义认为测量数据是固定的,根据测量数据可以得到我们对参数的认知程度 (参数的概率分布),得到了参数的概率分布也就求解了参数。
同样采用上述线性拟合的例子,需要估计的参数的概率分布可如下表示:
\begin{equation}
P(a \mid d)
\end{equation}
即在观测数据 (d) 的条件下,参数 (a) 的概率分布是什么?怎么样才能得到参数的分布 ($P(a \mid d)$)?
这里需要引入贝叶斯定理,贝叶斯定理是贝叶斯估计的理论基础,可如下表示:
\begin{equation}
P(a \mid d) = \frac{P(a) P(d \mid a)}{P(d)}
\label{beyes}
\end{equation}
贝叶斯定理可以这样理解,$a$ 和 $d$ 同时发生的概率可如下表示:
\begin{equation}
P(a \cap d) = P(a) P(d \mid a) = P(d) P(a \mid d)
\end{equation}
即$a$和$d$同时发生的概率可表示为:发生 $a$ 的概率乘上 $a$ 发生的条件下 $b$ 发生的概率,反之亦然。通过 $a$ 和 $b$ 同时发生这一桥梁,就可以建立起 $P(d \mid a)$ 和 $P(a \mid d)$ 的联系。
根据公式 (\ref{beyes}),就可以达到我们的目的,求解 $P(a \mid d)$。但是,$P(a)$、$P(d \mid a)$、$P(d)$怎么知道呢?这里,我们先介绍这几个量的概念。
- $P(a \mid d)$:参数 $a$ 的后验概率,依据测量数据 $d$ 得到的结果,就是我们需要计算的量。
- $P(a)$:参数 $a$ 的先验概率,在获取测量数据 $d$ 之前,我们对 $a$ 的认知。
- $P(d \mid a)$:似然度,表示观测数据 $d$ 信息,形式上与似然函数 $\ell (d \mid a)$ 相同。
- $P(d)$: 标准化常量,观测数据 $d$ 独立于待估参数 $a$,对于$a$ 而言,$P(d)$ 可以认为是常数。
公式 (\ref{beyes}) 可以改写为:
\begin{equation}
P(a \mid d) \propto P(a) \ell(d \mid a)
\end{equation}
这里即包含了贝叶斯方法的基本思路:假定要估计的参数是服从一定分布的随机变量;根据待估参数的先验分布,并结合观测数据信息,应用贝叶斯定理求得待估参数的后验分布,并根据待估参数的后验分布得到待估参数的估计量。
这时候,唯一不清楚的是先验分布 $P(a)$。先验分布是人们对参数的主观认识,需要事先提供。如果有多个测量方法对同一事件进行了测量,我们可以采用其他方法的结果作为先验事实,给出先验分布;当先验事实不存在时,可以主观的选择先验分布,如常用的扁平先验:
\begin{equation}
P(a) \propto 1
\end{equation}
后验分布的计算往往是难以直接计算的,因此,贝叶斯方法往往需要采用随机模拟的方法来生成符合后验分布的样本,从而得到后验分布。这里采用贝叶斯估计中常用的抽样方法:MCMC。MCMC 的原理这里不详细叙述。根据后验分布的表达式,利用 MCMC 方法生成满足后验分布的样本,用这些样本来确定我们的待估参数。所得结果如下。
- $a_0$的分布:
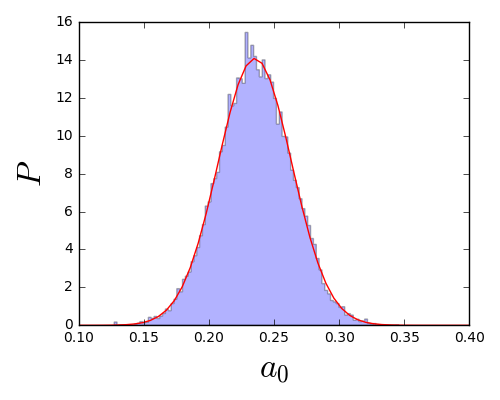
$a_1$的分布:
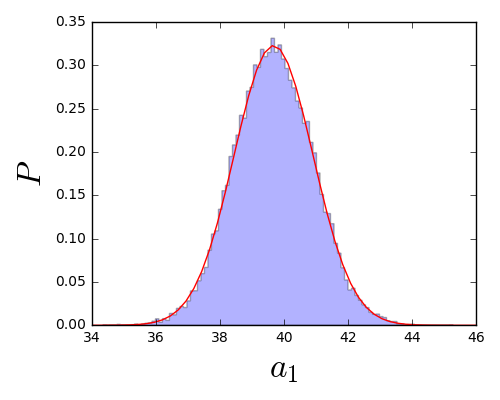
结果: