MCMC (1): 蒙特卡洛方法

Posted on | In

1. 蒙特卡洛方法

蒙特卡洛是用“模拟”解决问题的方法。具体来说，需要解决的问题是估计参数，该参数是某一随机事件的某个统计值，通过“模拟”大量该随机事件的样本，根据样本估计待估参数。

举个例子帮助理解：

怎么利用蒙特卡洛方法估计$pi$?

如下图所示：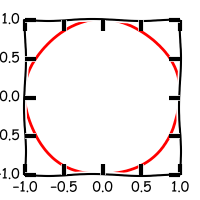

图中圆和正方形的面积比为：
\begin{equation*}
\frac{\pi r^2}{(2r)^2}=\frac{\pi}{4}
\end{equation*}
也就是说，只需要知道圆和它的外切正方形的面积比就可以求得 $\pi$。假设有这样的一个随机事件：

往正方形中撒入点，点落在正方形中的位置是均匀分布，随后计算有多少比例的点落入了圆中(根据距离圆心的距离判断)，这个比例就是 $\frac{\pi}{4}$。

上述过程就是蒙特卡洛方法，有以下三方面的内容：

  1. 随机事件：正方形中撒入点；
  2. 根据随机事件的概率分布(均匀分布)模拟数据，生成样本；
  3. 根据样本的某统计值(在圆内的比例)估计待估参数 $pi$。

一般地，蒙特卡洛方法的三个步骤为：

  1. 构造概率过程：确定随机事件的概率分布，该随机事件的某统计量刚好是待估参数；
  2. 采样：根据随机事件的概率分布采样；
  3. 估计参数：根据采样的样本估算参数。

2. PYTHON实现

利用蒙特卡洛法估计 $pi$，代码如下:

1
2
3
4
5
6
7
8
import numpy as np
n = 1000
x = 2.0*np.random.random(size=n)-1.0
y = 2.0*np.random.random(size=n)-1.0
index = [i for i in range(n) if (x[i]**2+y[i]**2) <1]
count = len(index)
pi = 4.0*count/n
print("PI=%f" %pi)

随机模拟了1000个点，所得结果为：PI=3.164。