1. 为什么需要马尔科夫链?
在上一篇文章 《MCMC (1): 蒙特卡洛方法》 中,我们总结了蒙特卡洛方法解决问题的三个步骤为:
- 构造概率过程;
- 采样;
- 估计参数。
马尔科夫链也就是需要解决上述的采样问题。
在计算机中,均匀分布 $Uniform(0,1)$ 的样本相对容易生成,常见的概率分布也可以基于均匀分布生成。但是,当我们的概率分布很复杂或者是高维分布时,样本的生成就存在困难,这时候就需要借助马尔科夫链了。也就是说,马尔科夫链的性质可以帮助我们近似的生成符合某概率分布的样本。为什么呢?
2. 马尔科夫链
马尔科夫链的定义很简单:
\begin{equation}
P(X_{t+1} = x \mid X_t, X_{t-1}, \cdots) =P(X_{t+1}=x \mid X_t)
\end{equation}
也就是状态转移的概率只依赖于前一个状态。符合这样定义的马氏链有什么性质呢?让我们看一个例子。
社会学家经常把人按其经济状况分成 3 类:低层、中层、高层 ,我们用 1、2、3 分别代表这三个阶层。社会学家们发现决定一个人的收入阶层只与其父母的收入阶层有关,也就说收入状态转移的概率只依赖于前一个状态(马尔科夫链)。具体的转移概率如下图所示: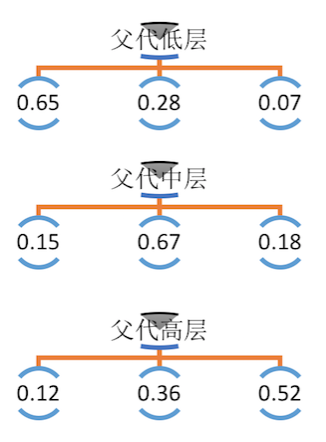
也就说如果一个人的父代的收入阶层是底层,他属于底层的概率是 0.65、属于中层的概率是 0.28、属于高层的概率是 0.07 (寒门难出贵子!)。将转移概率写成矩阵:
\begin{equation}
P =
\begin{bmatrix}
0.65 & 0.28 & 0.07 \\
0.15 & 0.67 & 0.18 \\
0.12 & 0.36 & 0.52 \\
\end{bmatrix}
\end{equation}
假设某一代为初始状态,初始概率分布为 $\pi_0 = [0.21,0.68,0.11]$,则根据转移矩阵我们可以计算 $n$ 代人的收入阶层分布:
| 下层比例 | 中层比例 | 高层比例 | |
|---|---|---|---|
| 第0代人 | 0.210 | 0.680 | 0.110 |
| 第1代人 | 0.252 | 0.554 | 0.194 |
| 第2代人 | 0.270 | 0.512 | 0.218 |
| 第3代人 | 0.278 | 0.497 | 0.225 |
| 第4代人 | 0.282 | 0.492 | 0.226 |
| 第5代人 | 0.284 | 0.490 | 0.226 |
| 第6代人 | 0.285 | 0.489 | 0.225 |
| 第7代人 | 0.286 | 0.489 | 0.225 |
| 第8代人 | 0.286 | 0.489 | 0.225 |
| 第9代人 | 0.286 | 0.489 | 0.225 |
| 第10代人 | 0.286 | 0.489 | 0.225 |
我们发现从第7代人开始,这个分布就稳定不变了,这个是偶然的吗?
我们换一个初始概率分布 $\pi_0 = [0.75,0.15,0.1]$ 试试:
| 下层比例 | 中层比例 | 高层比例 | |
|---|---|---|---|
| 第0代人 | 0.750 | 0.150 | 0.100 |
| 第1代人 | 0.522 | 0.346 | 0.132 |
| 第2代人 | 0.407 | 0.426 | 0.167 |
| 第3代人 | 0.349 | 0.459 | 0.192 |
| 第4代人 | 0.318 | 0.475 | 0.207 |
| 第5代人 | 0.303 | 0.482 | 0.215 |
| 第6代人 | 0.295 | 0.485 | 0.220 |
| 第7代人 | 0.291 | 0.487 | 0.222 |
| 第8代人 | 0.289 | 0.488 | 0.224 |
| 第9代人 | 0.288 | 0.488 | 0.224 |
| 第10代人 | 0.287 | 0.488 | 0.225 |
| 第11代人 | 0.287 | 0.488 | 0.225 |
| 第12代人 | 0.287 | 0.488 | 0.225 |
从上面的两个表格可以发现,两次分布都收敛了,而且都收敛到 $\pi=[0.286, 0.489, 0.225]$ 这个分布。这就是马尔科夫链的收敛性质。
这里我们不过多的讲述关于马尔科夫链的定理和性质,需近一步了解的可以参考本文后列出的参考资料。我们需要知道的是,对于一个概率分布来说,如果马尔科夫链中的每一步都让这个概率分布保持不变,我们就说这个概率分布是马尔科夫链的平稳分布。用公式可如下表示:
\begin{equation}
\pi P = \pi, \quad \sum_{i=0}^{\infty} \pi_i = 1
\end{equation}
其中 $\pi$ 是马尔科夫链的概率分布,$P$ 是转移概率矩阵。即概率分布乘上转移矩阵还是它本身,也就是概率分布在每一步都保持不变。而且 $\pi$ 是方程 $\pi P = \pi$ 的唯一非负解。
回到我们的正题。我们需要利用马尔科夫链的性质来生成复杂概率分布 $p(x)$ 的样本。很自然的,我们的想法是产生一条马氏链,使得它的平稳分布就是想要的分布。即,构造符合条件的转移矩阵,使其满足:
\begin{equation}
p(x)Q = p(x)
\end{equation}
因为 $p(x)$ 是上式的唯一解,我们可以根据上式来生成 $p(x)$ 的样本。
那么,如何构造转移矩阵呢?
假设我们有一个转移矩阵 $Q$($q(i,j)$),其满足如下条件:
\begin{equation}
p(i)q(i,j) = p(j)q(j,i)
\label{dbc}
\end{equation}
$i,j$ 是分布中的两个状态,如上面例子中的低层、中层(就是 $Q$ 矩阵中的下标)。根据 (\ref{dbc}) 式,我们有:
\begin{align}
& \sum_{i=1}^\infty p(i)q(i,j) = \sum_{i=1}^\infty p(j)q(j,i)
= p(j) \sum_{i=1}^\infty q(j,i) = p(j) \\
& \Rightarrow p Q = p
\end{align}
可以看到,只要构造满足 (\ref{dbc}) 式的转移矩阵,我们就可以得到平稳分布 $p$,(\ref{dbc}) 式也就是马氏链的细致平稳条件。根据 (\ref{dbc}) 式,利用随机采样的方法,就可以得到分布 $p$ 的样本。随机采样的方法将在下一章记录。
参考资料
[1] LDA-math-MCMC 和 Gibbs Sampling
[2] Information Theory, Inference, and Learning Algorithms, David J.C. MacKay. (Chap. 29).
[3] Pattern Recognition and Machine Learning, Christopher M. Bishop. (Chap. 11).