1. MCMC采样算法

在上一篇文章《MCMC (2): 马尔科夫链》中，我们提到需要构造一个转移矩阵 $Q(q(i,j))$，使其满足细致平稳条件：
\begin{equation}
p(i)q(i,j) = p(j)q(j,i)
\label{dbc}
\end{equation}

假设我们已经有一个转移矩阵为 $Q$ 的马氏链，$q(i,j)$ 表示从状态 $i$ 转移到 $j$ 的概率，通常情况下，我们随便取得转移矩阵不满足细致平稳条件，即：
\begin{equation}
p(i) q(i,j) \neq p(j) q(j,i)
\end{equation}
也就是说，这个转移矩阵不是所需要的。我们通过对其改造一下，使其满足细致平稳条件，如引入一个参数 $\alpha(i,j)$，使得：
\begin{equation}
p(i) q(i,j)\alpha(i,j) = p(j) q(j,i)\alpha(j,i)
\label{equ3}
\end{equation}
按照对称性，我们有：
\begin{equation}
\alpha(i,j)= p(j) q(j,i)， \quad \alpha(j,i) = p(i) q(i,j)
\end{equation}
于是，我们得到了满足细致平稳条件的转移矩阵 $Q’$:
\begin{equation}
Q’(i,j) = q(i,j)\alpha(i,j)
\end{equation}
在改造 $Q’$ 过程中引入的 $\alpha(i,j)$ 成为接受率，可以理解为从状态 $i$ 以 $q(i,j)$ 的概率跳转到状态 $j$ 的时候，我们以 $\alpha(i,j)$ 的概率接受这个转移，于是得到了新的马氏链的转移概率为 $Q’(i,j)=q(i,j)\alpha(i,j)$。

1.1. Metropolis采样方法

假设我们已经有一个转移矩阵 $Q$，将上述的理论实现为方法，具体过程为：

初始化马氏链状态，采样 $x_0$，其中 $x_0$ 服从 $\pi_0(x)$ 分布；
以 $x_0$ 为中心，根据转移矩阵 $q(x_1 \mid X=x_0)$ 采样 $x_1$，其中 $x_1$ 服从 $\pi_1(x)=\pi_0(x) Q$ 分布；
考虑到我们的转移矩阵不满足细致平稳条件，需要按照接受率 $\alpha(i,j)$ 确定是否接受从 $0$ 状态转移到 $1$ 状态；
若不接受，重新以 $x_0$ 为中心采样 $x_1$;
若接受，以 $x_1$ 为中心采样 $x_2$，其中 $x_2$ 服从 $\pi_2(x)=\pi_1(x) Q’$
重复以上过程，根据马氏链收敛定理，概率分布将收敛到 $\pi(x)$，即采样的 $x_n, x_{n+1}, x_{n+2}\cdots$将都服从 $\pi(x)$ 分布，而 $\pi(x)$ 正是我们需要采样的概率分布。这样，我们就得到了概率分布 $\pi(x)$ 的样本。

具体算法如下：
图1. 算法示意

1.2. MH 采样算法

上述的采样算法存在一个小问题：在马氏链的转移过程中，接受率可能偏小，这样采样过程容易原地踏步，收敛到平稳分布的速度过慢。为了扩大接受率，我们将 (\ref{equ3}) 式两边同时乘上一个系数，同比例的放大 $\alpha(i,j)$ 和 $\alpha(j,i)$, 使得两个数中最大的为 1，这样在满足细致平稳条件的情况下提高了接受率，这就是 Metropolis-Hastings 采样算法。
具体过程如下：
图2. 算法示意

2. MH算法 PYTHON 实现

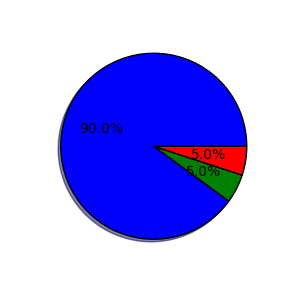
我们还是采用《MCMC (2): 马尔科夫链》中的例子，采样 $p = [0.9, 0.05, 0.05]$ 的分布的样本，即下层收入的人占比 90%，中层占比 5%，上层占比 5%。

import numpy as np
import matplotlib.pyplot as plt
p=np.array([0.9,0.05,0.05])
# 初始化转移矩阵 
A = np.array([p for x in range(len(p))], dtype=np.float32)
# 采样计数 
samplecount = 0
sMax = 100000
samples = []
# 马氏链初始状态
i = np.random.randint(len(p))
while True:
    # 以状态 i 为中心，根据转移矩阵采样状态 j
    j = np.argmax(np.random.multinomial(1, A[i]))
    # 计算接受率 (A[j][i]*p[j]) / (A[i][j]*p[i])
    alpha = min(1,(A[j][i]*p[j])/(A[i][j]*p[i]))
    # 生成u
    u = np.random.uniform()
    if u < alpha:
    	 # 转移至状态 j 
        i = j
        samplecount += 1
        samples.append(j)
    # if u > alpha, 状态不转移，依旧从状态 i 采样
    if samplecount >= sMax:
        break
    else:
        continue
        
samples = np.array(samples)
sizes = [np.sum(samples==0), np.sum(samples==1), np.sum(samples==2)]
plt.figure(figsize=[3,3])
plt.pie(sizes,autopct='%1.1f%%', shadow=True)

结果如下：
图3. 采样结果