1. 支持向量机

给定训练样本集 $\left { (x_i,y_i)\right }_{i=1}^N$，其中 $x_i \in \mathbb{R}^n $ 为特征空间，$y_i \in { -1,+1 }$ 为类标签。支持向量机是基于划分超平面 (separating hyperplane) 将数据分类的分类器。如图 1 所示，二维数据的线性划分超平面为一条直线。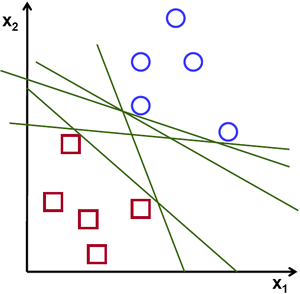
图1. 可以划分数据的划分超平面
可以看到，具有多个划分超平面可以将数据分类，我们需要找出唯一的划分超平面，使得划分效果最优，SVM 采用的是最大间隔 (maximum margin) 划分超平面。如图 2 所示。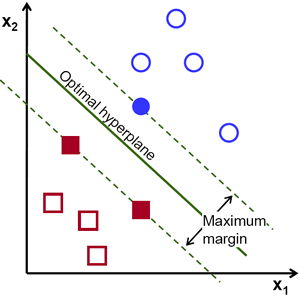
图2. 最大间隔划分超平面
图 2 中的实心点，刚好处在划分超平面上，这些点确定了划分超平面，称之为支持向量。

上面的例子为线性分类器，即超平面可以用一个线性方程表示：
\begin{equation}
\mathbf{w}^T \cdot \mathbf{x} +b= 0
\end{equation}

对于需要非线性超平面才能分离的数据，SVM 采用核方法，这也是要引入对偶问题最大的原因。

先基于线性可分支持向量机讲述原理，之后说明线性不可分支持向量机，
最后说明非线性支持向量机。

2. 线性可分支持向量机

2.1. 最大间隔超平面

上面提到支持向量机的最优划分标准是最大间隔。在特征空间中，划分超平面可用如下线性方程表示:
\begin{equation}
\mathbf{w}^T \cdot \mathbf{x} +b= 0
\end{equation}
其中 $\mathbf{w}$ 为超平面的法向量，$b$ 为位移项。样本点 $x_i$ 到划分超平面的几何距离为：
\begin{equation}
\gamma_i = \frac{|\mathbf{w} \cdot x_i +b|}{||\mathbf{w}||}
\label{eqn3}
\end{equation}
$||\mathbf{w}||$ 为 $\mathbf{w}$ 的 $L_2$ 范数。
假设超平面能够将训练样本正确分类，即若 $\mathbf{w} \cdot x_i +b >0$，则 $y_i = 1$，反之亦然。所以 (\ref{eqn3}) 式可以去掉绝对值，几何距离重写为：

\begin{equation}
\gamma_i = y_i\frac{\mathbf{w} \cdot x_i +b}{||\mathbf{w}||}
\end{equation}

我们定义训练集中最小的几何距离为几何间隔：
\begin{equation}
\gamma = \min \gamma_i
\end{equation}
最大间隔思想就是最大化几何间隔，在满足所有样本点的几何距离大于几何间隔的条件下：
\begin{equation}
\begin{split}
&\max_{\mathbf{w},b}\gamma \ &s.t. \ \ y_i\frac{\mathbf{w} \cdot x_i +b}{||\mathbf{w}||} \ge \gamma, \ \ i = 1,2,…,N
\end{split}
\label{eqn6}
\end{equation}
为了简化问题，我们引入一个新的定义，函数间隔：
\begin{equation}
\widehat{\gamma} = \frac{\gamma }{||\mathbf{w}||}
\end{equation}
所以，(\ref{eqn6}) 式重写为：

\begin{equation}
\begin{aligned} &\max_{\mathbf{w},b} \frac{\widehat{\gamma }}{||\mathbf{w}||} \ &s.t. \ \ y_i\left ( \mathbf{w}\cdot x_i + b \right ) \ge \widehat{\gamma }, \ \ i = 1,2,…,N \end{aligned}
\label{eqn8}
\end{equation}
可以看到，我们自由缩放函数间隔 $N$ 倍：
\begin{equation}
N ~\widehat{\gamma} = N~ y_i (\mathbf{w} \cdot x_i +b)
\end{equation}
超平面 $\mathbf{w}^T \cdot \mathbf{x} +b= 0$ 与缩放后的平面 $N~(\mathbf{w}^T \cdot \mathbf{x} +b)= 0$ 相同；几何间隔同样也不会变化。也就是说，任意缩放函数间隔，对于我们最大化几何间隔问题的解算没有影响。为了简化我们的问题，令函数间隔 $\widehat{\gamma}=1$，这也是引入函数间隔的原因。(\ref{eqn8}) 式简化为：

\begin{equation}
\begin{aligned} &\max_{\mathbf{w},b} \frac{ 1 }{||\mathbf{w}||} \ &s.t. \ \ y_i\left ( \mathbf{w}\cdot x_i + b \right ) \ge 1, \ \ i = 1,2,…,N \end{aligned}
\end{equation}

注意到最大化 $\frac{ 1 }{||\mathbf{w}||}$ 等价于最小化 $\frac{ 1 }{2}||\mathbf{w}||^2$，最终，SVM 需要解决的问题为以下有约束的最优化问题，更具体地，该问题为凸二次规划问题：
\begin{equation}
\begin{aligned} &\min_{\mathbf{w},b} \frac{ 1 }{2}||\mathbf{w}||^2 \ &s.t. \ \ y_i\left ( \mathbf{w}\cdot x_i + b \right ) \ge 1, \ \ i = 1,2,…,N \end{aligned}
\label{eqn11}
\end{equation}

2.2. 对偶问题

凸二次规划问题可以使用现成的优化计算包计算，为了引入核函数和方便计算，将原问题转为其对偶问题进行求解。

2.2.1. 原始问题

将原问题 (\ref{eqn11}) 式重写为：
\begin{equation}
\begin{aligned} &\min_{\mathbf{w},b} \frac{ 1 }{2}||\mathbf{w}||^2 \ &s.t. \ \ g(\mathbf{w},b) \le 0 , \ \ i = 1,2,…,N \end{aligned}
\label{eqn12}
\end{equation}
其中 $g(\mathbf{w},b)=1- y_i\left ( \mathbf{w}\cdot x_i + b \right )$。
首先，定义拉格朗日函数为：

\begin{equation}
L(\mathbf{w},b,\alpha) = \frac{1}{2} ||\mathbf{w}||^2 - \sum_{i=1}^N \alpha_i ~g(\mathbf{w},b)
\end{equation}
其中，$\alpha_i \ge 0$。引入 $(\mathbf{w},b)$ 的函数，记为：

\begin{equation}
\theta_p(\mathbf{w},b) = \max_{\alpha} L(\mathbf{w},b,\alpha)
\end{equation}
若上式最大化问题有解，其必满足 (\ref{eqn12}) 式的条件，且其解为：

\begin{equation}
\frac{ 1 }{2}||\mathbf{w}||^2 = \max_{\alpha} L(\mathbf{w},b,\alpha)
\end{equation}
因为 $\alpha_i \ge 0$，需要 $g(\mathbf{w},b) \le 0$ 才能有最大值解。

所以，原问题等价于如下问题：

\begin{equation}
\min_{\mathbf{w},b} \max_{\alpha} L(\mathbf{w},b,\alpha)
\end{equation}

2.2.2 原始问题的对偶问题

记原始问题的对偶问题为：
\begin{equation}
\max_{\alpha} \min_{\mathbf{w},b}L(\mathbf{w},b,\alpha)
\end{equation}
记:
\begin{equation}
\theta_d(\alpha) = \min_{\mathbf{w},b} L(\mathbf{w},b,\alpha)
\end{equation}
我们要通过对偶问题的求解来解决原始问题，那么我们的问题是：对偶问题的解和原始问题的解有什么关系呢？

2.2.3 原始问题与对偶问题的关系

对任意的 $(\mathbf{w},b,\alpha)$，有：

\begin{equation}
\theta_d(\alpha) = \min_{\mathbf{w},b} L(\mathbf{w},b,\alpha) \le L(\mathbf{w},b,\alpha) \le \max_{\alpha} L(\mathbf{w},b,\alpha) = \theta_p(\mathbf{w},b)
\end{equation}

若原始问题和对偶问题都有解，根据上式，有：

\begin{equation}
\begin{split}
&\theta_d(\alpha) \le \theta_p(\mathbf{w},b) \\
&\Rightarrow \max_{\alpha} \theta_d(\alpha) \le \min_{\mathbf{w},b}\theta_p(\mathbf{w},b) \\
&\Rightarrow \max_{\alpha} \min_{\mathbf{w},b}L(\mathbf{w},b,\alpha) \le \min_{\mathbf{w},b} \max_{\alpha} L(\mathbf{w},b,\alpha)
\end{split}
\end{equation}
即对偶问题的解小于或等于原始问题的解。在什么情况下，对偶问题的解与原始问题的解相同呢？如果能找到这个条件，那么我们直接解决对偶问题就可以得到原始问题的解，这个条件就是 KKT (Karush-Kuhn-Tucker) 条件。

KKT 条件为：

\begin{equation}
\begin{split}
\nabla_\mathbf{w} L(\mathbf{w}^*,b^*,\alpha^*) &= 0 \
\nabla_b L(\mathbf{w}^*,b^*,\alpha^*) &= 0 \
\nabla_\alpha L(\mathbf{w}^*,b^*,\alpha^*) &= 0 \
\alpha_i^* ~ g(\mathbf{w}^*,b^*) &= 0, i=1,2,…,N \
g(\mathbf{w}^*,b^*) &\le 0, i=1,2,…,N \
\alpha_i^* &\ge 0, i=1,2,…,N
\end{split}
\end{equation}

如果 $(\mathbf{w}^*,b^*,\alpha^*)$ 满足 KKT 条件，则对偶问题和原始问题的解均为 $(\mathbf{w}^*,b^*,\alpha^*)$。

\begin{equation}
\begin{split}
& \max_\alpha \min_{\mathbf{w},b}L(\mathbf{w},b,\alpha) \
&= \max_{\alpha} L(\mathbf{w}^*,b^*,\alpha) \
& = L(\mathbf{w}^*,b^*,\alpha^*) \
& = \frac{1}{2} ||\mathbf{w^*}||^2 - \sum_{i=1}^N \alpha_i^* ~g(\mathbf{w^*},b^*) \
& = \min_{\mathbf{w},b} \frac{ 1 }{2}||\mathbf{w}||^2 \ \ s.t. \ \ g(\mathbf{w^*},b^*) \le 0 , \ \ i = 1,2,…,N
\end{split}
\end{equation}

所以，SVM 问题转化为 KKT 条件下的对偶问题求解。

2.2.3 对偶问题的求解

为了得到对偶问题的解，需要先求 $L(\mathbf{w},b,\alpha)
$ 对 $(\mathbf{w},b)$ 的极小，再求对 $\alpha$ 的极大。

求$\min \limits_{\mathbf{w},b}L(\mathbf{w},b,\alpha)$
将 $L(\mathbf{w},b,\alpha)$ 分别对 $\mathbf{w}$，$b$ 求偏导数并令其等于 $0$：
\begin{equation}
\begin{aligned} \frac{\partial L(\mathbf{w},b,a)}{\partial \mathbf{w}} &= 0 \Rightarrow \mathbf{w} - \sum_{i=1}^N a_iy_ix_i = 0 \ \frac{\partial L(\mathbf{w},b,a)}{\partial b} &= 0 \Rightarrow - \sum_{i=1}^N a_i~y_i = 0 \end{aligned}
\end{equation}
将上式带入拉格朗日函数消去 $\mathbf{w}$，$b$，有：
\begin{equation}
\begin{aligned}
\min_{\mathbf{w},b}L(\mathbf{w},b,\alpha) = \ &-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^Na_i a_jy_iy_j (x_i \cdot x_j) + \sum _{i=1}^Na_i \
& \ s.t. \ \ \ \sum_{i=1}^N a_iy_i = 0 \end{aligned}
\end{equation}
求对偶问题
\begin{equation}
\begin{aligned} &\max_{a_i} \ -\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^Na_i a_jy_iy_j (x_i \cdot x_j) + \sum _{i=1}^Na_i\ & \ s.t. \ \ \ \sum_{i=1}^N a_iy_i = 0 \end{aligned}
\end{equation}

根据上式，可以求取对偶问题的解 $\alpha^*$，再根据 KKT 的条件求取原始问题的解 $(\mathbf{w}^*,b^*)$，从而可以得到划分超平面，这种算法为对偶学习算法。

对偶问题的解是一个凸二次规划问题，理论上任何一个凸二次规划问题的软件包都可以解决，但是通常很慢，为了能够更快找到好的解，我们采用 SMO 算法。该算法的原理先放一放。

3. 线性不可分支持向量机

上述的问题是基于所有样本点 $(x_i, y_i)$ 都能满足函数间隔大于等于 $1$ 的约束条件，即线性可分的。如果存在异常点不满足约束条件，上面的方法就不适用了。为了解决线性不可分的问题，可以对每个样本引入一个松弛变量 $\xi _i \ge 0$，使得函数间隔加上松弛变量大于等于 $1$，即约束条件变为：
\begin{equation}
y_i(\mathbf{w} \cdot x_i +b) \ge 1 – \xi_i
\end{equation}
显然，$\xi_i$ 不能任意大，否则所有样本点都满足约束条件，为了约束 $\xi_i$ 的大小，需要在目标函数中加入惩罚。最终，优化目标改成如下的形式：

\begin{equation}
\begin{aligned} &\min_{\mathbf{w},b,\xi}\ \ \frac{1}{2}||\mathbf{w}||^2 + C\sum_{i=1}^N \xi_i \ &s.t. \ \ \ \ -y_i(\mathbf{w} \cdot x_i + b) -\xi_i + 1\le 0, \ \ i = 1,2,…,N \ &\ \ \ \ \ \ \ \ \ \ -\xi_i \le 0 ,\ \ i = 1,2,…,N \end{aligned}
\end{equation}
其中，$C > 0$ 称为惩罚参数，一般由应用问题决定，$C$ 值越大对误分类的惩罚越大。

同样地，线性不可分支持向量机的学习问题也是凸二次规划问题，我们采用与线性可分支持向量机同样的方法，即：

构造拉格朗日函数；
原始问题转化为对偶问题；
利用 KKT 条件消去其他参数，得到只包含参数 $a_i$ 的对偶问题；
利用 SMO 算法解释出 $a_i$；
根据 KKT 条件和 $a_i$ 解算出 $\mathbf{w}~,b,$。

这里给出对偶问题的具体形式：
\begin{equation}
\begin{aligned} &\min_a \ \ \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N a_ia_jy_iy_j(x_i \cdot x_j) - \sum_{i=1}^Na_i \ &s.t. \ \ \ \ \ 0 \le a_i \le C , \ i = 1,2,…,N\ & \ \ \ \ \ \ \ \ \ \sum_{i=1}^Na_iy_i = 0,\ i = 1,2,…,N \end{aligned}
\end{equation}

可以看到，线性可分支持向量机可以认为是松弛变量等于$0$，也就是上式的特例。线性可分和线性不可分支持向量机合称为线性支持向量机。至此，上式就是线性支持向量机待学习的问题。

4. 线性支持向量机算法

构造约束最优化问题：
\begin{aligned} &\min_a \ \ \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N a_ia_jy_iy_j(x_i \cdot x_j) - \sum_{i=1}^Na_i \ &s.t. \ \ \ \ \ 0 \le a_i \le C , \ i = 1,2,…,N\ & \ \ \ \ \ \ \ \ \ \sum_{i=1}^Na_iy_i = 0,\ i = 1,2,…,N \end{aligned}
采用 SMO 算法求解 $a_, ~i = 1,2,….N$；
根据 KKT 条件和 $a_i^*$ 解算出 $\mathbf{w}^*~,b^*,$。
\begin{aligned}
&\mathbf{w}^* = \sum_{i=1}^Na_i^*y_ix_i\ &b^* = y_j - \sum_{i=1}^N y_ia_i^*(x_i \cdot x_j) \\
&0 < a^*_j < C
\end{aligned}
得到超平面 $\mathbf{w}^* \cdot x + b^* = 0$。对于需要分类的数据，根据 $f(x) = sign(\mathbf{w}^* \cdot x+b^*)$ 判断其类别，其中 $sign$ 为相应的决策函数。

5. 非线性支持向量机

对于给定的非线性可分数据集 $\left { (x_i,y_i)\right }_{i=1}^N$，找不到一个分类平面将数据集分类。自然的想法就是将数据映射到新的空间 $\mathbf{x} \rightarrow \phi(\mathbf{x})$，使得其在新的空间中存在分类平面 $\mathbf{w}^T \cdot \phi(\mathbf{x}) +b= 0$，将其分类。如图 3 所示。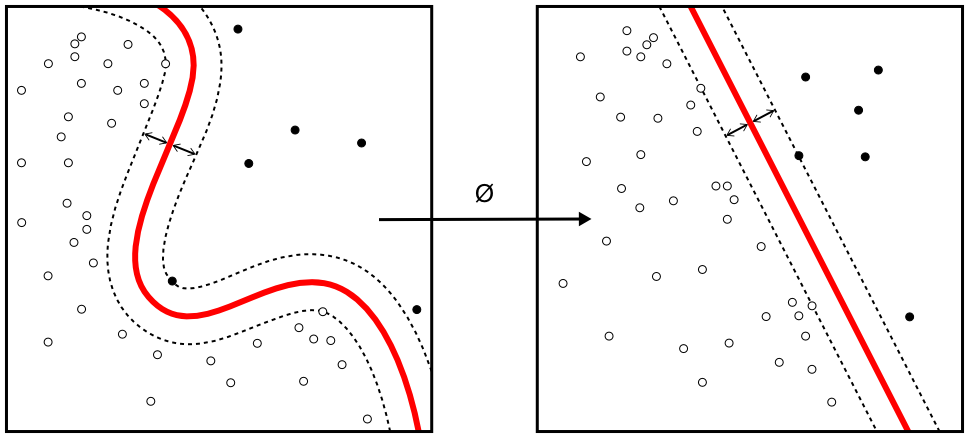
图3. 左边为非线性可分，投影之后线性可分.

通常来说，非线性 SVM 不显式地定义映射函数 $\phi(\mathbf{x})$，而是采用核技巧，原因下面讲。

5.1. 核技巧

针对非线性可分数据集，假设找到了映射函数 $\phi(\mathbf{x})$，使其线性可分。与线性支持向量机推导一样，约束最优化问题为：

\begin{equation}
\begin{aligned} &\min_a \ \ \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N a_ia_jy_iy_j\color{red}{(\phi{(x_i)}^T \cdot \phi{(x_j)})}- \sum_{i=1}^Na_i \ &s.t. \ \ \ \ \ 0 \le a_i \le C , \ i = 1,2,…,N\ & \ \ \ \ \ \ \ \ \ \sum_{i=1}^Na_iy_i = 0,\ i = 1,2,…,N \end{aligned}
\end{equation}
可以看到，上式的优化问题需要计算 $K(x_i,x_j)= \phi{(x_i)}^T \cdot \phi{(x_j)}$，我们称 $K(x_i,x_j)$ 为核函数。因为特征空间通常很高维，甚至是无穷维，映射函数的内积 $\phi{(x_i)}^T \cdot \phi{(x_j)}$ 并不容易计算。为了避开这个障碍，特征空间的內积用核函数 $K(,)$ 来代替，从而避免高维中的內积。所以，不需要定义映射函数 $\phi{\mathbf{x}}$，只需要定义核函数，这便是核技巧。核技巧的好处在于不需要显式定义映射函数，只需要选择合适的核函数。此外，值得说明的是，正是对偶问题的引入，才能使得应用核技巧。

5.2. 核函数

显然，若已知映射函数，则可写出核函数。但是现实任务中我们通常不知道映射函数是什么样的形式。那么，什么样的函数 $K(,)$ 可以作为一个有效的核函数呢？答案是只要 $K(,)$ 满足 Mercer 定理即可。这里不再展开叙述。

定义了核函数，实际上就定义了一个新的特征空间，这个新的特征空间称之为再生核希尔伯特空间。需要注意的是，在不知道特征映射的形式时，我们并不知道什么样的核函数是合适的，而核函数也仅是隐式的定义了新的特征空间。于是，核函数的选用成为了非线性支持向量机的最大变数。若核函数选择不合适，则意味着数据映射到了一个不合适的特征空间，很可能会导致分类效果不佳。

显然，判断一个函数是否可以当成核函数或者判断一个核函数是否适合是很困难的。这里给出一些常用的核函数。

线性核
\begin{equation*}
K(x_i,x_j) = x_i^T~x_j +c
\end{equation*}
多项式核
\begin{equation*}
K(x_i,x_j) = (x_i^T~x_j +c)^d
\end{equation*}
高斯核
\begin{equation*}
K(x_i,x_j) = exp(\frac{-||x_i-x_j||^2}{2\sigma^2})
\end{equation*}
拉普拉斯核
\begin{equation*}
K(x_i,x_j) = exp(\frac{-||x_i-x_j||}{\sigma})
\end{equation*}
此外，也可通过函数组合得到。

参考资料

[1] 《机器学习》, 周志华

[2] 《统计学习方法》, 李航

[3] 《Convex Optimization》, Stephen Boyd and Lieven Vandenberghe