1. k 近邻概述
k 近邻法是一种常用的监督学习方法。给定一个训练集,其中样本的类别已定。分类时,基于某种距离度量找出训练集中与其最靠近的 k 个训练样本,然后根据这 k 个样本的类别通过多数表决等方式进行预测。k 近邻法不具有显式的训练过程,是懒惰学习 (lazy learning) 的著名代表。其中,关键的内容为距离度量和 k 值的选择。
1.1 距离度量
常用的距离度量有闵可夫斯基距离:
\begin{equation}
L_p(x_i,x_j)=(\sum_{l=1}^n|x_i^{(l)}-x_j^{(l)}|^p)^{1/p}
\end{equation}
$p=2$ 时,欧式距离:
\begin{equation}
L_p(x_i,x_j)=(\sum_{l=1}^n|x_i^{(l)}-x_j^{(l)}|^2)^{1/2}
\end{equation}$p=1$ 时,曼哈顿距离:
\begin{equation}
L_p(x_i,x_j)=\sum_{l=1}^n|x_i^{(l)}-x_j^{(l)}|
\end{equation}$p=\infty$ 时,切比雪夫距离:
\begin{equation}
L_p(x_i,x_j)=\max_l |x_i^{(l)}-x_j^{(l)}|
\end{equation}
1.2. k 值的选择
k 值的选择会对结果产生重大影响。
k 值选择较小,则分类结果容易因为噪声点的干扰而出现错误。换句话说,k 值较小意味模型复杂,容易过拟合。
k 值选择较大,意味着与输入样本较远的训练样本也会对结果起作用,使得预测结果错误。
通常做法是利用交叉验证评估一系列不同的 k 值,选取结果最好的 k 值作为训练参数。
2. kd 树
现在我们有了 k 近邻的思想。对于一个输入样本,我们怎么样选取它的 k 个近邻呢?
最简单的方法就是线性扫描,计算输入样本和训练集中每一个样本的距离。但是当训练样本很大时,这种方法是不可取的。
为了提高 k 个近邻的搜索速度,可以采用特殊的结构存储训练数据,这里介绍 kd 树方法。
2.1. kd 树的构造
kd 树是一种对 k 维空间样本点进行存储的树形数据结构,表示对 k 维空间的划分。构造 kd 树的过程相当于用垂直于某一维度的超平面将 k 维空间切分。
构造平衡 kd 树的过程如下:
- 在训练集中选择具有最大方差的维度 k,然后在该维度上选择中位数为切分点,对该数据集合进行划分,得到两个子集合,划分的超平面为过切分点且垂直于 k 维度坐标轴的超平面;同时,将落在划分超平面上的样本点保存为根节点。
- 对两个子集重复
1步骤,直至所有子集合不能再划分为止;如果某个子集合不能划分,则将该子集合中的数据保存到叶子节点。
图 1 所示为 kd 树构造过程,数据来源于 wikipedia。首先在维度 $X^{(0)}$ 上选取切分点 A,分为两个子集合,并把 A 保存为根节点…………。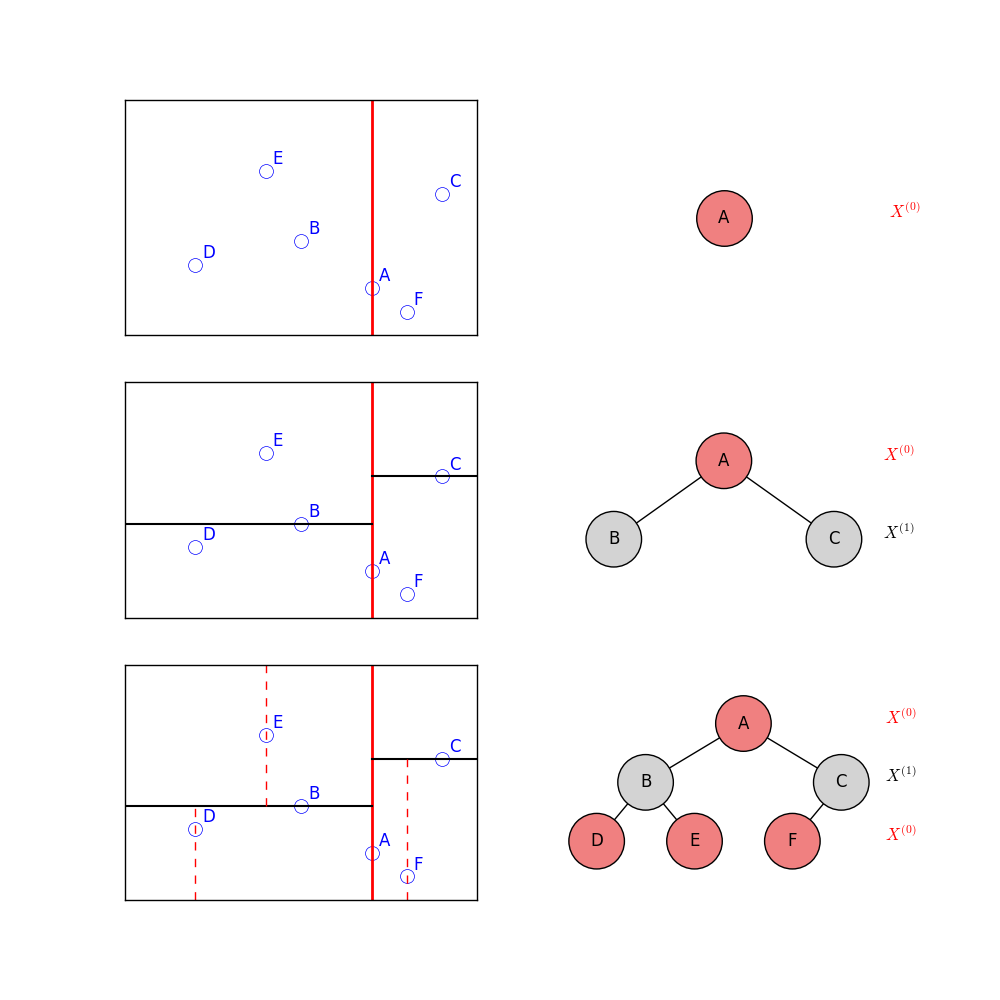
2.2. kd 树搜索
假设已经构造了 kd 树,我们有一个新的输入 $x$,搜索它的最近邻。
其算法如下:
- 在 kd 树中找出包含目标点 $x$ 的叶结点:从根结点出发,递归的向下访问 kd 树。比较当前维上 $x$ 与切分点的坐标,若小移动到左子结点,否则右边,知道叶结点为止;
- 将到达的叶节点记为“当前最近点”,离目标点的距离为最近距离;
递归向上回溯,在每个结点作如下操作:
3.1 如果该结点上的样本离目标点更远,向上回溯;
3.2 如果该结点上的样本距离目标点更近,将该结点标记为当前最近点,更新最近距离;并检查该结点的另一子结点对应的区域是否与以目标点为球心,最近距离为半径的超球体相交。若相交,移动到另一个子节点,向下落到叶节点,递归地进行最近邻搜索。若不相交,向上回溯。当回退到根节点时,搜索结束。
参考资料
[1] 《机器学习》, 周志华
[2] 《统计学习方法》, 李航