1. Boosting
Boosting 是一族将弱学习器提升为强学习器的算法。工作机制类似:
- 从初始训练集中训练出一个基学习器;
- 根据基学习器的表现调整样本的权值,使得先前基学习器做错的样本权值更大;
- 然后基于调整之后的权值训练下一个基学习器;
- 反复学习,得到一系列基学习器,组合这些基学习器。
对于 Boosting 算法来说,关键点在于以下两个问题:
- 如何改造权值?
- 如果组合基学习器?
Boosting 族算法最著名的代表是 AdaBoost。
2. AdaBoost 算法
简单来说,AdaBoost 算法就是根据指定参数 $M$,进行 $M$ 轮训练,得到 $M$ 个弱学习器 $G_i$ 及每个弱学习器的权重 $\alpha_i$,最终将这些弱学习器进行线性组合得到最终的学习器 $G$。
给定训练样本集 $\left { (x_i,y_i)\right }_{i=1}^N$,其中 $x_i \in \mathbb{R}^n $ 为特征空间,$y_i \in { -1,+1 }$ 为类标签。 AdaBoost 算法流程如下:
(1). 初始化训练集的权值分布:
\begin{equation}
D_{1}=(w_{11},…,w_{1i},…,w_{1N}),~w_{1i}=\frac{1}{N},~i=1,2,…,N
\end{equation}
(2) 对 $m=1,2,3…,M$:
(2.1) 使用权值分布 $D_m$ 的训练集学习,得到基学习器:
\begin{equation}
G_{m}(x):~X{\rightarrow}{-1,+1}
\end{equation}
(2.2) 计算 $G_{m}(x)$ 在训练集上的误差率:
\begin{equation}
e_{m}=P(G_{m}(x_{i})\neq y_{i}) =\sum_{i=1}^n w_{mi}I(G_{m}(x_{i})\neq y_{i})
\end{equation}
其中,
\begin{equation}
I(G_{m}(x_{i})\neq y_{i}) =
\left{
\begin{array}{ccc}
0,~ G_{m}(x_{i})&=& y_i \
1,~ G_{m}(x_{i})&\neq& y_i
\end{array}
\right.
\end{equation}
(2.3) 计算 $G_{m}(x)$ 的系数:
\begin{equation}
\alpha_{m}=\frac{1}{2}log \frac{1-e_{m}}{e_{m}}
\end{equation}
如图 1 所示,基学习器误差越大,其系数越小。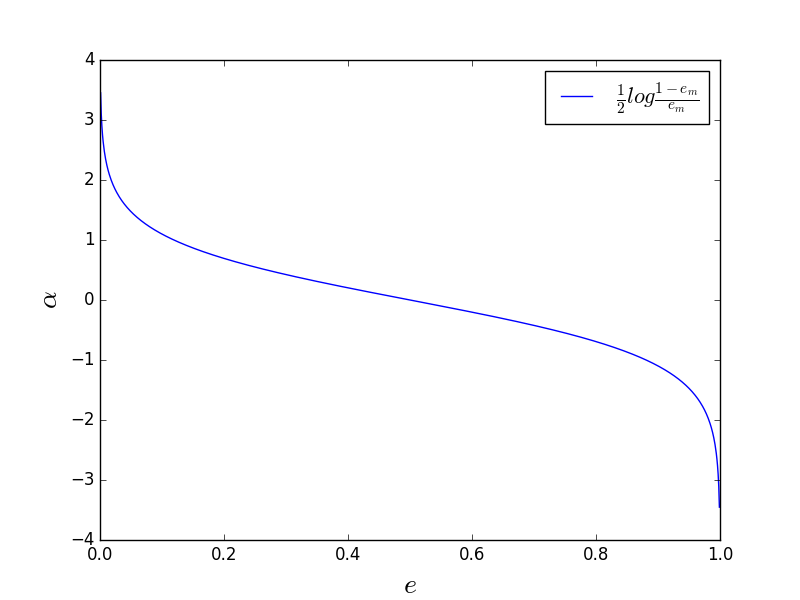
(2.4) 更新训练集的权值分布:
\begin{equation}
\begin{split}
& D_{m+1}=(w_{m+1,1},…,w_{m+1,i},…,w_{m+1,N}) \\
& w_{m+1,i}= \left{
\begin{array}{ccc}
\frac{w_{mi}}{Z_{m}}~ e^{-\alpha_i},~ G_{m}(x_{i})&=& y_i \
\frac{w_{mi}}{Z_{m}}~ e^{\alpha_i},~ G_{m}(x_{i})&\neq& y_i
\end{array}
\right.
\end{split}
\end{equation}
其中,
\begin{equation}
Z_{m} = \sum_{i=1}^{N}w_{mi}exp(-\alpha_{m}y_{i}G_{m}(x_{i}))
\end{equation}
为归一化因子。
(3) 构建线性分类器的线性组合:
\begin{equation}
f(x)=\sum_{m=1}^{M}\alpha_{m}G_{m}(x)
\end{equation}
得到最终分类器:
\begin{equation}
G(x)=sign(f(x))=sign(\sum_{m=1}^{M}\alpha_{m}G_{m}(x))
\end{equation}
3. AdaBoost 的解释之损失函数优化
上一节提及到了学习器系数和权值更新公式,但是没有解释这个公式的来源,其实它们可以从从损失函数优化问题的角度来解读。
AdaBoost 还有另一个解释,即可以认为 Adaboost 是模型为加法模型,学习算法为前向分步学习算法,损失函数为指数函数的分类问题。
3.1. 加法模型
加法模型 (additive model) 为:
\begin{equation}
f(x) = \sum_{m=1}^M \beta_m b(x; \gamma_m)
\end{equation}
其中,$b(x; \gamma_m)$ 为基函数,$\gamma_m$ 为基函数的参数,$\beta_m$ 为基函数的系数。
很明显,AdaBoost 的最终分类器等价于加法模型。现在的问题是该怎么样得到最终分类器,也就是其中的参数呢?
3.2. 指数损失函数优化
AdaBoost 的损失函数是指数损失函数,即求得的最终分类器:
\begin{equation}
f(x)=\sum_{m=1}^{M}\alpha_{m}G_{m}(x)
\end{equation}
满足最小化指数损失函数:
\begin{equation}
L(y,f(x)) = e^{-yf(x)}
\end{equation}
通常这是一个复杂的优化问题。需要采用前向分布算法来求解。
3.3 前向分布算法
前向分布算法的思想是:因为学习的是加法模型,如果能够从前向后,每一步只学习一个基函数及其系数,逐步逼近目标函数,那么就可以简化优化的复杂度。
AdaBoost 第一个基分类器是直接将基学习器算法用于初始训练集得到;此后利用前一个弱学习器的结果,迭代生成权值和基学习器系数,生成后一个弱学习器。第 $m$ 轮的学习器与第 $m-1$ 轮的学习器有如下关系:
\begin{equation}
f_{m}(x) = f_{m-1}(x) + \alpha_m G_m(x)
\end{equation}
目标是每一轮的学习过程中得到 $\alpha_m$ 和 $G_m(x)$,使得 $f_m(x)$ 的指数损失最小,从而最终分类器的指数损失最小。
根据前向分布学习算法的关系,第 $m$ 轮得到的损失函数为:
\begin{equation}
\begin{split}
&arg ~\min_{\alpha_m, G_m} e^{-y f_m{(x)}}\\
&=arg ~\min_{\alpha_m, G_m} e^{-y~(f_{m-1}(x)+\alpha_m G_m(x) )}\\
&=arg ~\min_{\alpha_m, G_m} \sum_{i=1}^N e^{-y_i~(f_{m-1}(x_i)+\alpha_m G_m(x_i) )}
\end{split}
\end{equation}
令 $w_{mi} = e^{-y_i~f_{m-1}(x_i)}$,它的值不依赖于 $\alpha_m$、$G_m(x)$,仅仅依赖于 $f_{m-1}$,随着每一轮迭代而改变。
先求得 $G^*_m(x)$,再上式对 $\alpha_m$ 求导,得到:
\begin{equation} \alpha^*{m}=\frac{1}{2}log \frac{1-e{m}}{e_{m}} \end{equation}
也就是上文的 (5) 式,即学习器系数。
根据 (13) 式和 $w_{mi} = e^{-y_i~f_{m-1}(x_i)}$,有:
\begin{equation} \begin{split} w_{m+1,i}= \left{ \begin{array}{ccc} w_{mi}~ e^{-\alpha_i},~ G_{m}(x_{i})&=& y_i \ w_{mi}~ e^{\alpha_i},~ G_{m}(x_{i})&\neq& y_i \end{array} \right. \end{split} \end{equation}
其与 (6) 式的权值更新公式只差归一化因子,因而等价。
以上,就是 AdaBoost 的另一种解释。
参考资料
[1] 《机器学习》, 周志华
[2] 《统计学习方法》, 李航