1. 支持向量机
给定训练样本集 $\left { (x_i,y_i)\right }_{i=1}^N$,其中 $x_i \in \mathbb{R}^n $ 为特征空间,$y_i \in { -1,+1 }$ 为类标签。支持向量机是基于划分超平面 (separating hyperplane) 将数据分类的分类器。如图 1 所示,二维数据的线性划分超平面为一条直线。
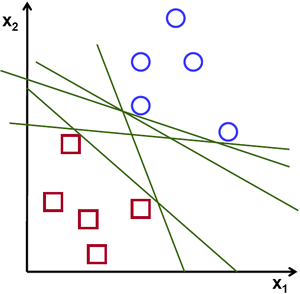
可以看到,具有多个划分超平面可以将数据分类,我们需要找出唯一的划分超平面,使得划分效果最优,SVM 采用的是最大间隔 (maximum margin) 划分超平面。如图 2 所示。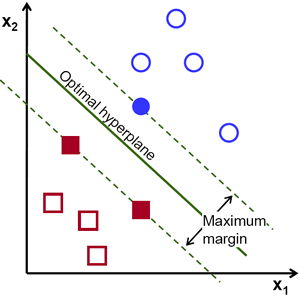
图 2 中的实心点,刚好处在划分超平面上,这些点确定了划分超平面,称之为支持向量。
在样本空间中,划分超平面可以用一个线性方程表示:
\begin{equation}
\mathbf{w}^T \cdot \mathbf{x} +b= 0
\end{equation}
样本点 $x_i$ 到划分超平面的几何距离为:
\begin{equation}
\gamma_i = \frac{|\mathbf{w} \cdot x_i +b|}{||\mathbf{w}||}
\end{equation}
$||\mathbf{w}||$ 为 $\mathbf{w}$ 的 $L_2$ 范数。