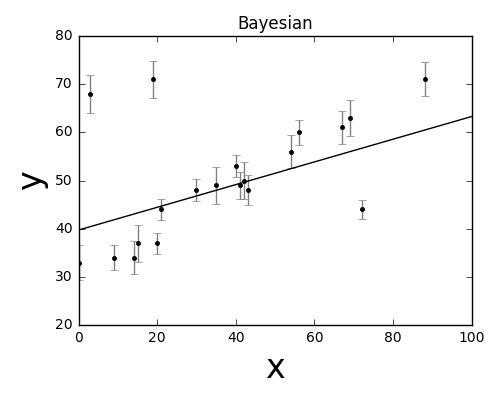
1. 贝叶斯决策论

考虑一个简单的二分类问题，假设有一个输入向量 $x$，我们的目标是对于 $x$ 预测它的类别 $y$，其中 $y = {C_1, C_2}$。现在我们有一个算法对 $x$ 进行了分类，这个算法会把输入空间划分为不同的区域 $R_k$，区域 $R_k$ 中的所有点都被分类为 $C_k$。假设现在我们有个输入，根据算法它被划分在区域 $R_1$，即我们的决策结果为 $C_1$，但实际上它是 $C_2$ 类，这样我们就犯了分类错误，反之亦然。在决策过程中，我们希望能最小化错误分类率 $p(mistake)$：
\begin{equation}
\begin{split}
p(mistake) &= p( x \in R_1,C_2) + p( x \in R_2,C_1)
\\
&= \int_{R_1} p(C_2,x) ~dx +\int_{R_2} p(C_1,x) ~dx
\end{split}
\end{equation}
即 $R_1$ 区域中，实际类别为 $C_2$ 的样本尽量少；$R_2$ 区域中，实际类别为 $C_1$ 的样本尽量少。

实际情况中，我们面对的情况要比最小化错误率复杂，因为把 $C_1$ 类错分了 $C_2$ 类和把 $C_2$ 类错分为 $C_1$ 类的代价是不一样。我们需要对不同的错误加一个权值，这就是期望损失 (expected loss)：
\begin{equation}
EL = \int_{R_1} \color{red}{\lambda_{21}}~ p(C_2,x) ~dx +\int_{R_2}\color{red}{\lambda_{12}}~ p(C_1,x) ~dx
\end{equation}
其中，$\lambda_{21}$ 是将一个真实标记为 $C_1$ 误分类为 $C_2$ 的损失，反之同理。

更一般地，对于 $K$ 类的问题，期望损失为：
\begin{equation}
EL = \sum_{k} \sum_{j} \int_{R_j} \lambda_{kj}~~p( C_k, x)~ dx
\end{equation}

对于每一个样本 $x$，我们要将其划分到决策区域 $R$ 中，那么划分到 $R_1$ 还是 $R_2$ ……中呢？我们希望期望损失能够最小化。也就是说，对于每个 $x$，我们将其划分到 $R_j$ 中，这样的结果下其期望损失最小：
\begin{equation}
arg~ \min ~\sum_k~\lambda_{kj}~p( C_k, x)
\end{equation}

将联合概率形式写成条件概率：
\begin{equation}
arg~ \min ~\sum_k~\lambda_{kj}~p(C_k \mid x)~p(x)
\label{5}
\end{equation}

注意到 $p(x)$ 对于所有项都相同，最小化 (\ref{5}) 式等价于：
\begin{equation}
arg~ \min ~\sum_k~\lambda_{kj}~p(C_k \mid x)
\label{6}
\end{equation}

2. 后验概率最大化

若我们的损失函数简化为：
\begin{equation}
\lambda_{kj} = \begin{cases}1,&k≠j\0,&k=j\end{cases}
\end{equation}
(\ref{6}) 式等价于：
\begin{equation}
\begin{split}
f(x) &= arg~ \min ~\sum_k~\lambda_{kj}~p(C_k \mid x) \\
& = arg~ \min ~\sum_{k\neq j}~ p(C_k \mid x)
\\
& = arg~ \min ~[1- p(C_{k = j} \mid x)]
\\
& = arg \max p(C_j \mid x)
\end{split}
\end{equation}
对于每个 $x$，我们将其划分到 $R_j$ 中，最大化 $p(C_j \mid x)$ 就能够使得期望损失最小化。也就是说，后验概率最大等价于 $0-1$ 损失函数时的期望损失最小。记决策结果为 $c= R_j$，我们需要最大化 $p(c \mid x)$。在现实任务中，$p(c \mid x)$ 通常难以直接获取，需要使用贝叶斯公式。

基于贝叶斯定理，有：
\begin{equation}
p(c \mid x) = \frac{p(c) ~p(x \mid c)}{p(x)}
\end{equation}
其中 $p(c \mid x)$ 称之为后验概率。

3. 朴素贝叶斯分类器

为了得到我们的模型，需要最大化后验概率，因为：
\begin{equation} p(c \mid x) \propto p(c) ~p(x \mid c) \end{equation}
最大化后验概率等价于：
\begin{equation}
\label{11}
arg \max p(c) ~p(x \mid c) \end{equation}
也就是需要估计先验概率 $p(c)$ 和类条件概率 $p(x \mid c)$。针对具体问题，类条件概率 $p(x \mid c)$ 是所有特征 $x$ 上的联合概率，难以从有限的样本直接估计而得。为避开这个问题，朴素贝叶斯分类器采用了特征独立性假设：即对已知类别，假设所有属性相互独立。基于该假设，(\ref{11}) 式重写为：
\begin{equation}
arg \max p(c) ~\prod_{i=1}^d p(x_i \mid c)
\end{equation}

因此，朴素贝叶斯分类器的训练过程就是基于数据集 D 来估算先验概率 $p(c)$ 和每个属性的条件概率 $p(x_i \mid c)$。

假设训练过程已经完成，有一个新的输入 $x={x_1, x_2, x_3\cdots}$，需要采用朴素贝叶斯来进行二分类 $y = {0,1}$，其过程为：

• 根据训练的结果：先验概率和每个属性的条件概率，计算 $p(0) ~\prod\limits_{i=1}^d p(x_i \mid 0)$；
• 根据训练的结果：先验概率和每个属性的条件概率，计算 $p(1) ~\prod\limits_{i=1}^d p(x_i \mid 1)$；
• 那个大划分为那类。

参考资料

[1] 《机器学习》, 周志华

[2] Pattern Recognition and Machine Learning, Christopher M. Bishop.

1. 决策树概述

决策树是一种基本的分类和回归算法。其根据数据的特征，采用树结构进行决策的方法。通常包括 3 个步骤：

• 特征划分选择
• 决策树生成
• 剪枝处理

一般地，一颗决策树包含一个根节点，若干内部节点和若干叶节点。其算法的基本流程如下，其中 D 为数据集，A 为特征集：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def creatTree(D, A):
	根据 D 生成叶节点集 node  # 数据标记
	if len(node)==1:       # D 中样本属于同一类别
		标记所有数据为同一叶节点
	if A == [] or len(D.feature)==1 # D 中只有一个特征
		将 node 标记为叶节点，其 label 为 D 中样本数量最多的类
	#
	从 A 中挑出最优特征 a
	#
	for value in a:
		生成新的特征集 A* = (A-a)
		生成新的数据集 D* 表示 D 中取值为 value 的样本子集
		if D* == []
			将 node 标记为叶节点，其 label 为 D* 中样本数量最多的类
		else:
			creatTree(D*, A*)
	return tree

可以看到，算法第 8 行是决策树算法最关键的内容，即特征划分的选择：怎么选出最优特征。

2. 特征划分选择

我们希望采用某个值，按照该值可以对 A 中的特征进行排序，自然就选出了最优的特征。

2.1. 信息增益

假定当前数据集 D 中第 $k$ 类样本所占比例为 $p_k$，则 D 的信息熵为：
\begin{equation}
entropy(D) = -\sum_{k=1}^n p_k log_2 p_k
\end{equation}
假设属性 $a$ 有 $V$ 个取值，记 $D^v$ 为取值为 $a^v$ 的样本子集。用属性 $a$ 划分数据集所获得的信息增益为：
\begin{equation}
Gain(D,a) = entropy(D) - \sum^V_1 \frac{|D^v|}{D}entropy(D^v)
\label{id3}
\end{equation}
信息熵代表信息的混沌程度，信息增益的含义为：数据的混沌程度减去用 $a$ 划分后的数据混沌程度，划分后的数据集混沌程度越小，信息增益越大。因此我们可以用信息增益作为准则来选择最优特征。

2.2. ID3

ID3 就是采用公式 (\ref{id3}) 作为准则来划分特征的。

2.3. C4.5

信息增益偏好于取值数目较多的特征，为了减少这种偏好，C4.5 采用增益率作为划分特征的准则：
\begin{equation}
Gain-Ratio(D,a) = \frac{Gain(D,a)}{IV(a)}
\label{c4.5}
\end{equation}
其中：
\begin{equation}
IV(a) = -\sum_1^V \frac{|D^v|}{D} log_2 \frac{|D^v|}{D}
\end{equation}
与 $a$ 的取值数目成正比，因此，增益率准则偏好于取值数目较少的特征，为了减少这种偏好，C4.5 并不是直接采用增益率作为划分准则，而是分为两步：

1. 找出信息增益高于平均水平的属性；
2. 从上述属性集中选取增益率最高的属性。

2.4 CART

CART 采用基尼指数作为划分准则。基尼指数定义为：
\begin{equation}
Gini-Index(D,a) = \sum_1^V \frac{|D^v|}{D} Gini(D^v)
\end{equation}
其中，基尼值定义为：
\begin{equation}
Gini(D) = 1 - \sum_1^n p^2_k
\end{equation}
表示从数据集 D 中随机抽取两个不一样的样本的概率。

3. 剪枝处理

剪枝是为了处理过拟合，基本策略有：

• 预剪枝：在决策树生成过程中，对每个节点划分前先进行估计，若不能带来泛化性能提升，则停止划分；
• 后剪枝：先生成一颗完整的树，自下而上的对非叶节点进行估计，若该节点对应的子树替换成叶节点能带来泛化性能提升，则将子树替换为叶节点。

预剪枝有可能引起欠拟合，后剪枝通常比预剪枝保留更多分支。一般来说，后剪枝剪枝效果好但是时间花销大。

参考资料

[1] 《机器学习》, 周志华

1. MCMC采样算法

在上一篇文章 《MCMC (2): 马尔科夫链》 中，我们提到需要构造一个转移矩阵 $Q(q(i,j))$，使其满足细致平稳条件：
\begin{equation}
p(i)q(i,j) = p(j)q(j,i)
\label{dbc}
\end{equation}

假设我们已经有一个转移矩阵为 $Q$ 的马氏链，$q(i,j)$ 表示从状态 $i$ 转移到 $j$ 的概率，通常情况下，我们随便取得转移矩阵不满足细致平稳条件，即：
\begin{equation}
p(i) q(i,j) \neq p(j) q(j,i)
\end{equation}
也就是说，这个转移矩阵不是所需要的。我们通过对其改造一下，使其满足细致平稳条件，如引入一个参数 $\alpha(i,j)$，使得：
\begin{equation}
p(i) q(i,j)\alpha(i,j) = p(j) q(j,i)\alpha(j,i)
\label{equ3}
\end{equation}
按照对称性，我们有：
\begin{equation}
\alpha(i,j)= p(j) q(j,i)， \quad \alpha(j,i) = p(i) q(i,j)
\end{equation}
于是，我们得到了满足细致平稳条件的转移矩阵 $Q’$:
\begin{equation}
Q’(i,j) = q(i,j)\alpha(i,j)
\end{equation}
在改造 $Q’$ 过程中引入的 $\alpha(i,j)$ 成为接受率，可以理解为从状态 $i$ 以 $q(i,j)$ 的概率跳转到状态 $j$ 的时候，我们以 $\alpha(i,j)$ 的概率接受这个转移，于是得到了新的马氏链的转移概率为 $Q’(i,j)=q(i,j)\alpha(i,j)$。

1.1. Metropolis采样方法

假设我们已经有一个转移矩阵 $Q$，将上述的理论实现为方法，具体过程为：

1. 初始化马氏链状态，采样 $x_0$，其中 $x_0$ 服从 $\pi_0(x)$ 分布；
2. 以 $x_0$ 为中心，根据转移矩阵 $q(x_1 \mid X=x_0)$ 采样 $x_1$，其中 $x_1$ 服从 $\pi_1(x)=\pi_0(x) Q$ 分布；
3. 考虑到我们的转移矩阵不满足细致平稳条件，需要按照接受率 $\alpha(i,j)$ 确定是否接受从 $0$ 状态转移到 $1$ 状态；
4. 若不接受，重新以 $x_0$ 为中心采样 $x_1$;
5. 若接受，以 $x_1$ 为中心采样 $x_2$，其中 $x_2$ 服从 $\pi_2(x)=\pi_1(x) Q’$
6. 重复以上过程，根据马氏链收敛定理，概率分布将收敛到 $\pi(x)$，即采样的 $x_n, x_{n+1}, x_{n+2}\cdots$将都服从 $\pi(x)$ 分布，而 $\pi(x)$ 正是我们需要采样的概率分布。这样，我们就得到了概率分布 $\pi(x)$ 的样本。

具体算法如下：

1.2. MH 采样算法

上述的采样算法存在一个小问题：在马氏链的转移过程中，接受率可能偏小，这样采样过程容易原地踏步，收敛到平稳分布的速度过慢。为了扩大接受率，我们将 (\ref{equ3}) 式两边同时乘上一个系数，同比例的放大 $\alpha(i,j)$ 和 $\alpha(j,i)$, 使得两个数中最大的为 1，这样在满足细致平稳条件的情况下提高了接受率，这就是 Metropolis-Hastings 采样算法。
具体过程如下：

2. MH算法 PYTHON 实现

我们还是采用 《MCMC (2): 马尔科夫链》 中的例子，采样 $p = [0.9, 0.05, 0.05]$ 的分布的样本，即下层收入的人占比 90%，中层占比 5%，上层占比 5%。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

import numpy as np
import matplotlib.pyplot as plt
p=np.array([0.9,0.05,0.05])
# 初始化转移矩阵 
A = np.array([p for x in range(len(p))], dtype=np.float32)
# 采样计数 
samplecount = 0
sMax = 100000
samples = []
# 马氏链初始状态
i = np.random.randint(len(p))
while True:
    # 以状态 i 为中心，根据转移矩阵采样状态 j
    j = np.argmax(np.random.multinomial(1, A[i]))
    # 计算接受率 (A[j][i]*p[j]) / (A[i][j]*p[i])
    alpha = min(1,(A[j][i]*p[j])/(A[i][j]*p[i]))
    # 生成u
    u = np.random.uniform()
    if u < alpha:
    	 # 转移至状态 j 
        i = j
        samplecount += 1
        samples.append(j)
    # if u > alpha, 状态不转移，依旧从状态 i 采样
    if samplecount >= sMax:
        break
    else:
        continue
        
samples = np.array(samples)
sizes = [np.sum(samples==0), np.sum(samples==1), np.sum(samples==2)]
plt.figure(figsize=[3,3])
plt.pie(sizes,autopct='%1.1f%%', shadow=True)

结果如下：

1. 为什么需要马尔科夫链？

在上一篇文章 《MCMC (1): 蒙特卡洛方法》 中，我们总结了蒙特卡洛方法解决问题的三个步骤为：

• 构造概率过程；
• 采样；
• 估计参数。

马尔科夫链也就是需要解决上述的采样问题。

在计算机中，均匀分布 $Uniform(0,1)$ 的样本相对容易生成，常见的概率分布也可以基于均匀分布生成。但是，当我们的概率分布很复杂或者是高维分布时，样本的生成就存在困难，这时候就需要借助马尔科夫链了。也就是说，马尔科夫链的性质可以帮助我们近似的生成符合某概率分布的样本。为什么呢？

2. 马尔科夫链

马尔科夫链的定义很简单：

\begin{equation}
P(X_{t+1} = x \mid X_t, X_{t-1}, \cdots) =P(X_{t+1}=x \mid X_t)
\end{equation}

也就是状态转移的概率只依赖于前一个状态。符合这样定义的马氏链有什么性质呢？让我们看一个例子。

社会学家经常把人按其经济状况分成 3 类：低层、中层、高层 ，我们用 1、2、3 分别代表这三个阶层。社会学家们发现决定一个人的收入阶层只与其父母的收入阶层有关，也就说收入状态转移的概率只依赖于前一个状态(马尔科夫链)。具体的转移概率如下图所示：

也就说如果一个人的父代的收入阶层是底层，他属于底层的概率是 0.65、属于中层的概率是 0.28、属于高层的概率是 0.07 (寒门难出贵子！)。将转移概率写成矩阵：

\begin{equation}
P =
\begin{bmatrix}
0.65 & 0.28 & 0.07 \\
0.15 & 0.67 & 0.18 \\
0.12 & 0.36 & 0.52 \\
\end{bmatrix}
\end{equation}

假设某一代为初始状态，初始概率分布为 $\pi_0 = [0.21,0.68,0.11]$，则根据转移矩阵我们可以计算 $n$ 代人的收入阶层分布：

我们发现从第7代人开始，这个分布就稳定不变了，这个是偶然的吗？

我们换一个初始概率分布 $\pi_0 = [0.75,0.15,0.1]$ 试试：

从上面的两个表格可以发现，两次分布都收敛了，而且都收敛到 $\pi=[0.286, 0.489, 0.225]$ 这个分布。这就是马尔科夫链的收敛性质。

这里我们不过多的讲述关于马尔科夫链的定理和性质，需近一步了解的可以参考本文后列出的参考资料。我们需要知道的是，对于一个概率分布来说，如果马尔科夫链中的每一步都让这个概率分布保持不变，我们就说这个概率分布是马尔科夫链的平稳分布。用公式可如下表示：
\begin{equation}
\pi P = \pi, \quad \sum_{i=0}^{\infty} \pi_i = 1
\end{equation}
其中 $\pi$ 是马尔科夫链的概率分布，$P$ 是转移概率矩阵。即概率分布乘上转移矩阵还是它本身，也就是概率分布在每一步都保持不变。而且 $\pi$ 是方程 $\pi P = \pi$ 的唯一非负解。

回到我们的正题。我们需要利用马尔科夫链的性质来生成复杂概率分布 $p(x)$ 的样本。很自然的，我们的想法是产生一条马氏链，使得它的平稳分布就是想要的分布。即，构造符合条件的转移矩阵，使其满足：
\begin{equation}
p(x)Q = p(x)
\end{equation}
因为 $p(x)$ 是上式的唯一解，我们可以根据上式来生成 $p(x)$ 的样本。

那么，如何构造转移矩阵呢？

假设我们有一个转移矩阵 $Q$($q(i,j)$)，其满足如下条件：
\begin{equation}
p(i)q(i,j) = p(j)q(j,i)
\label{dbc}
\end{equation}
$i,j$ 是分布中的两个状态，如上面例子中的低层、中层(就是 $Q$ 矩阵中的下标)。根据 (\ref{dbc}) 式，我们有：
\begin{align}
& \sum_{i=1}^\infty p(i)q(i,j) = \sum_{i=1}^\infty p(j)q(j,i)
= p(j) \sum_{i=1}^\infty q(j,i) = p(j) \\
& \Rightarrow p Q = p
\end{align}
可以看到，只要构造满足 (\ref{dbc}) 式的转移矩阵，我们就可以得到平稳分布 $p$，(\ref{dbc}) 式也就是马氏链的细致平稳条件。根据 (\ref{dbc}) 式，利用随机采样的方法，就可以得到分布 $p$ 的样本。随机采样的方法将在下一章记录。

参考资料

[1] LDA-math-MCMC 和 Gibbs Sampling

[2] Information Theory, Inference, and Learning Algorithms, David J.C. MacKay. (Chap. 29).

[3] Pattern Recognition and Machine Learning, Christopher M. Bishop. (Chap. 11).

1. 蒙特卡洛方法

蒙特卡洛是用“模拟”解决问题的方法。具体来说，需要解决的问题是估计参数，该参数是某一随机事件的某个统计值，通过“模拟”大量该随机事件的样本，根据样本估计待估参数。

举个例子帮助理解：

怎么利用蒙特卡洛方法估计$pi$?

如下图所示：

图中圆和正方形的面积比为：
\begin{equation*}
\frac{\pi r^2}{(2r)^2}=\frac{\pi}{4}
\end{equation*}
也就是说，只需要知道圆和它的外切正方形的面积比就可以求得 $\pi$。假设有这样的一个随机事件：

往正方形中撒入点，点落在正方形中的位置是均匀分布，随后计算有多少比例的点落入了圆中(根据距离圆心的距离判断)，这个比例就是 $\frac{\pi}{4}$。

上述过程就是蒙特卡洛方法，有以下三方面的内容：

1. 随机事件：正方形中撒入点；
2. 根据随机事件的概率分布(均匀分布)模拟数据，生成样本；
3. 根据样本的某统计值(在圆内的比例)估计待估参数 $pi$。

一般地，蒙特卡洛方法的三个步骤为：

1. 构造概率过程：确定随机事件的概率分布，该随机事件的某统计量刚好是待估参数；
2. 采样：根据随机事件的概率分布采样；
3. 估计参数：根据采样的样本估算参数。

2. PYTHON实现

利用蒙特卡洛法估计 $pi$，代码如下:

1
2
3
4
5
6
7
8

import numpy as np
n = 1000
x = 2.0*np.random.random(size=n)-1.0
y = 2.0*np.random.random(size=n)-1.0
index = [i for i in range(n) if (x[i]**2+y[i]**2) <1]
count = len(index)
pi = 4.0*count/n
print("PI=%f" %pi)

随机模拟了1000个点，所得结果为：PI=3.164。

1. 频率主义与贝叶斯主义

频率主义认为概率与事件的频率有关，贝叶斯主义认为概率是对事件的认知程度的度量。举个例子说明一下，假设我们多次测量了一个棍子的长度，得到的观测数据为： Data = [L1, L2]，其中 L1 占比 30%，L2 占比 70%（假设测量结果就两种情况）。

• 频率主义认为：棍子的长度 (length) 是固定值，即参数是固定的。由于测量误差的存在，测量结果 L1 发生的频率为 30%，L2 发生的频率为 70%。根据频率主义者对概率的认知，可用如下公式表示：\begin{equation*}
  P(Data=L1 \mid length)= 30\% \\
  P(Data=L2 \mid length)= 70\%
  \end{equation*}
  其意义为：在 length 的条件下(在棍子长度为固定某值得条件下)，得到 L1 的概率为 30%，得到 L2 的概率为 70%。

• 贝叶斯主义认为：观测结果 (Data) 是固定的，是我们对事件的认知。根据观测结果，棍子长度为 L1 的概率为 30%，为 L2 的概率为7 0%，即参数 (length) 不是固定的，而是一个分布。概率就是我们对棍子长度的认知程度，我们 30% 地认为棍子长度为 L1, 70% 地认为棍子长度为 L2，可用如下公式表示：
  \begin{equation*}
  P(length=L1 \mid Data)= 30\% \\
  P(length=L2 \mid Data)= 70\%
  \end{equation*}
  其意思为：在观测数据 (Data) 的条件下，棍子长度为 L1 的概率为 30%，为 L2 的概率为 70%。

为了更直观的说明频率主义和贝叶斯主义，根据上述例子，有如下图像。

$\quad$

2. 频率主义参数估计

我们用线性拟合作为例子，考虑下面的数据集合 x、y和y 的误差 e，数据来源于Frequentism and Bayesianism II: When Results Differ。

先看一下数据长什么样。

我们的任务是找出一条直线来拟合数据，这里我们采用最大似然估计法(常用的最小二乘估计为最大似然估计的一种特例：正态最大似然估计)。

我们构造一个线性模型，参数有斜率和截距，模型定义如下：
\begin{equation}
\label{model}
\hat{y} = a_0x+a_1
\end{equation}
根据观测数据 x，y 集合，估计 $a=(a_0,a_1)$。
对于某一次测量值 ($d_i=(x_i,y_i,e_i)$)，假设测量误差按正态分布，该事件发生的概率分布满足：
\begin{equation}
\label{pro}
P(d_i \mid a) = \frac{1}{\sqrt{2\pi e_i^2}}exp[-\frac{(y_i-\hat{y}_i)^2}{2e_i^2}]
\end{equation}

似然函数为每个观测值概率的乘积：
\begin{equation}
\label{like}
\ell (d \mid a) = \prod_{i=1}^N P(d_i \mid a)
\end{equation}

最大似然法就是使似然函数最大，这里很好理解。还是使用上面棍子的例子，假设我们测得的数据为 (10.1 米, 9.9 米)，根据测量数据我们估计棍子到底多长。那怎么估计呢？考虑这样的一个问题：棍子长度为多少时，我们最大概率上得到的测量数据为 (10.1 米, 9.9 米)，答案呼之欲出，我们猜测棍子的长度为 10.0 米，因为这样我们最大概率获得了我们的观测数据。如果棍子长度为 1 米，我们基本上不可能得到(10.1 米, 9.9 米)这样的观测数据。也就是说，我们需要求一个 length，使得 $P(10.1 \mid length)\cdot P(9.9 \mid length)$ 最大，也就是最大似然法。

回到上面的线性拟合问题，我们需要估计参数 $a$，使得 $d$ 发生的概率最大。一般情况下，因为似然估计值可能非常小，通常更方便的做法是取似然函数的对数，将公式 (\ref{pro}) 代入公式 (\ref{like}) 并取对数：
\begin{equation}
\begin{split}
log \ell (d \mid a) = -\frac{1}{2}\sum_{i=1}^N[log(2\pi e_i^2)+ \frac{(y_i-\hat{y}_i)^2}{e_i^2}]
\end{split}
\end{equation}

\begin{equation}
log \ell (d \mid a) = const - \sum_{i=1}^N\frac{1}{2e_i^2}(y_i-\hat{y}_i^2)
\end{equation}

我们需要求解 $a$ 使得上式最大化，等价于最小化下式:
\begin{equation}
loss = \sum_{i=1}^N\frac{1}{2e_i^2}(y_i-\hat{y})
\label{loss}
\end{equation}

上式与我们的直觉很符合，为了找到一个最佳拟合直线，我们需要观测值与模型值的差的平方和最小，这也就是最小二乘方法，或者说最小平方损失。

公式 (\ref{loss}) 的解算方法很多，这里用矩阵的解算方法。记误差 $e^2$ 组成的矩阵为 $P$，$v= y_i-\hat{y}$ 组成的矩阵为 $V$，公式 (\ref{loss}) 最小化等价于：
\begin{equation}
V^T P V = min
\label{vpv}
\end{equation}

将 $v= y_i-\hat{y}$ 写成矩阵形式：
\begin{equation}
V = Ba -l
\end{equation}

其中，$a=[a_0, a_1]$，$l=[-y]$，$B=[-x, -1]$。

求解公式 (\ref{vpv}):
\begin{equation}
\begin{split}
&\frac{\partial{V^TPV}}{\partial a}=2V^T P \frac{\partial V}{\partial{a}}= V^TPB=0 \\
&\Rightarrow B^TPV=0 \\
&\Rightarrow B^TP(Ba-l)=0 \\
&\Rightarrow a = (B^TPB)^{-1}B^TPl
\end{split}
\end{equation}

根据上式，即可利用频率主义的方法估计参数 $a$。所得结果如下图所示：

总结：频率主义认为参数是固定的(斜率和截距)，利用最大似然法估计参数，使得在此参数条件下，得到该组观测数据的概率最大。

3. 贝叶斯主义参数估计

贝叶斯主义认为测量数据是固定的，根据测量数据可以得到我们对参数的认知程度 (参数的概率分布)，得到了参数的概率分布也就求解了参数。

同样采用上述线性拟合的例子，需要估计的参数的概率分布可如下表示：
\begin{equation}
P(a \mid d)
\end{equation}

即在观测数据 (d) 的条件下，参数 (a) 的概率分布是什么？怎么样才能得到参数的分布 ($P(a \mid d)$)？

这里需要引入贝叶斯定理，贝叶斯定理是贝叶斯估计的理论基础，可如下表示：
\begin{equation}
P(a \mid d) = \frac{P(a) P(d \mid a)}{P(d)}
\label{beyes}
\end{equation}

贝叶斯定理可以这样理解，$a$ 和 $d$ 同时发生的概率可如下表示：
\begin{equation}
P(a \cap d) = P(a) P(d \mid a) = P(d) P(a \mid d)
\end{equation}

即$a$和$d$同时发生的概率可表示为：发生 $a$ 的概率乘上 $a$ 发生的条件下 $b$ 发生的概率，反之亦然。通过 $a$ 和 $b$ 同时发生这一桥梁，就可以建立起 $P(d \mid a)$ 和 $P(a \mid d)$ 的联系。

根据公式 (\ref{beyes})，就可以达到我们的目的，求解 $P(a \mid d)$。但是，$P(a)$、$P(d \mid a)$、$P(d)$怎么知道呢？这里，我们先介绍这几个量的概念。

• $P(a \mid d)$：参数 $a$ 的后验概率，依据测量数据 $d$ 得到的结果，就是我们需要计算的量。
• $P(a)$：参数 $a$ 的先验概率，在获取测量数据 $d$ 之前，我们对 $a$ 的认知。
• $P(d \mid a)$：似然度，表示观测数据 $d$ 信息，形式上与似然函数 $\ell (d \mid a)$ 相同。
• $P(d)$： 标准化常量，观测数据 $d$ 独立于待估参数 $a$，对于$a$ 而言，$P(d)$ 可以认为是常数。

公式 (\ref{beyes}) 可以改写为：
\begin{equation}
P(a \mid d) \propto P(a) \ell(d \mid a)
\end{equation}

这里即包含了贝叶斯方法的基本思路：假定要估计的参数是服从一定分布的随机变量；根据待估参数的先验分布，并结合观测数据信息，应用贝叶斯定理求得待估参数的后验分布，并根据待估参数的后验分布得到待估参数的估计量。

这时候，唯一不清楚的是先验分布 $P(a)$。先验分布是人们对参数的主观认识，需要事先提供。如果有多个测量方法对同一事件进行了测量，我们可以采用其他方法的结果作为先验事实，给出先验分布；当先验事实不存在时，可以主观的选择先验分布，如常用的扁平先验：
\begin{equation}
P(a) \propto 1
\end{equation}

后验分布的计算往往是难以直接计算的，因此，贝叶斯方法往往需要采用随机模拟的方法来生成符合后验分布的样本，从而得到后验分布。这里采用贝叶斯估计中常用的抽样方法：MCMC。MCMC 的原理这里不详细叙述。根据后验分布的表达式，利用 MCMC 方法生成满足后验分布的样本，用这些样本来确定我们的待估参数。所得结果如下。

• $a_0$的分布：

• $a_1$的分布：

  

• 结果：

  

参考资料

[1] Frequentism and Bayesianism 系列博文

1. 卷积

卷积是通过两个函数生成第三个函数的一种数学算子：
\begin{equation}
y(\color{red}{t})= \int_{-\infty}^{\infty} x(\tau) h(t-\tau) d\color{blue}{\tau}
\end{equation}

我们先什么都不要管，只需要注意，不要把公式中的 $\color{red}{t}$ 和 $\color{blue}{\tau}$ 混淆了。

2. 卷积的解释

贴近生活的解释永远比公式更好理解，参考网上卷积的各种血腥残暴的解释。这里，我们使用一个温和的例子。

假设你是一名研究生，你还有三天的时间来完成老板的任务，由于患有拖延症，你工作的热情可如下图表示：

上面就是你的输入函数 $x(t)$，具体内容为:
\begin{equation*}
x(0) = 0.1, \quad
x(1) = 0.1, \quad
x(2) = 0.6.
\end{equation*}

按照你这个效率，完全不可能完成任务，因此老板会每天苦口婆心的来 push 你。老板的 push 就是 $h(t)$ 函数，我们称之为响应函数。基本上，随着时间的流逝，老板的劝说只是浪费了一点口水，对你的作用越来越小。所以，我们的 $h(t)$ 函数应该长这样：

$h(t)$ 的具体内容为:
\begin{equation*}
h(0) = 8, \quad
h(1) = 3, \quad
h(2) = 2.
\end{equation*}

意思就是老板当天的劝说对你的作用是8倍，过了一天后为3倍，过了两天后为2倍。也就是说，$h$ 函数作用于工作热情上的效果是这样的：对当天工作热情的效果是 8 倍，对昨天工作热情的效果是 3 倍，对前天工作热情的效果是 2 倍。其他时候我们记为 $h^{+}=0$

那在老板的 push 下，我们的工作热情是怎么样的呢？

这里就是输入函数在响应的作用下，得到输出函数的问题，也就是求卷积。说了这么多，好像只是介绍了我们的 $x$ 和 $h$ 函数，卷积到底是什么意思呢？让我们看一下 $x$ 和 $h$ 的卷积会发生什么。

• Day 0：今天不太想工作，只有 0.1 的意愿，但是老板来 push 了，最终的工作意愿为：
  \begin{equation*}
  \begin{split}
  y(0) &= \int_0^2 x(\tau)h(0-\tau)d\tau \\
  &= \color{red}{x(0)}h(0) + \color{blue}{x(1)}h^+ +\color{blue}{x(2)}h^+ \\
  &= \color{red}{x(0)}h(0) =0.8
  \end{split}
  \end{equation*}
  该公式的意思可以这样理解：将 $h$ 函数作用在输入上，得到了我们的输出。根据 $h$ 函数的特性，它只作用在今天、昨天和前天的数据上 (以 $y(0)$ 中的 $0$ 为参考)，对于明天 ($x(1)$) 和后天的数据 ($x(2)$) 的数据没有作用。

• Day 1: 昨天老板骂了一顿，今天又来了，老板昨天的效果也还在。最终，我们的工作热情为：
  \begin{equation*}
  \begin{split}
  y(1) &= \color{blue}{x(0)}h(1)+\color{red}{x(1)}h(0)+\color{blue}{x(2)}h^+ \\
  &= 0.8+0.3=1.1
  \end{split}
  \end{equation*}
  意思就是今天你的工作热情只有 0.1，老板把你骂了后，你的热情变成了0.8；除此之外，老板昨天劝说的效果还在，只是从 8 倍的作用变成了 3 倍。按照 $h$ 函数的作用，将所有输入结果叠加。

• Day 2：同样的：
  \begin{equation*}
  \begin{split}
  y(2) &= \color{blue}{x(0)}h(2)+\color{blue}{x(1)}h(1)+\color{red}{x(2)}h(0) \\
  &=4.8+0.3+0.2=5.3
  \end{split}
  \end{equation*}
  我们可以把 $h$ 看做权，这个计算实际上就相当于对 $x$ 进行了加权叠加。

• Day 3: 虽然从今天开始我们不再有新的工作热情(输入数据)，但是思想教育的效果依然余留，工作效率在老板 push 的作用下为：
  \begin{equation*}
  \begin{split}
  y(3) &= \color{blue}{x(0)}h^++\color{blue}{x(1)}h(2)+\color{blue}{x(2)}h(1) \\
  &=1.8 + 0.2 = 2
  \end{split}
  \end{equation*}
  幸好，根据 $h$ 的加权作用，老板第一天的教育终于被你忘了。

• Day 4: 快要迎来美好时光，老板前几天的教育都要被你忘了。
  \begin{equation*}
  \begin{split}
  y(3) &= \color{blue}{x(0)}h^++\color{blue}{x(1)}h^++\color{blue}{x(2)}h(2) \\
  &=1.2
  \end{split}
  \end{equation*}
  老板的督促使得你保持了几天工作热情。根据你三分钟热度的性格，今天之后，又过上了毫无工作热情的生活。

我们复习一下卷积的公式：
\begin{equation}
y(\color{red}{t})= \int_{-\infty}^{\infty} x(\tau) h(t-\tau) d\color{blue}{\tau}
\end{equation}

从上面的例子可以看出，卷积就是对于每一个位置 $t_i \in (-\infty,\infty)$，将输入 $x$ (整个输入，上面几式中颜色标注)，按照 $h$ 的方式加权叠加起来，这里 $h$ 的方式就是以当前时间为基准 ($t_i$，红色标注)，对当天的效应是 8，昨天的效应是 3，前天的效应是 2。

最后，给出在老板的连番督促下，你的工作热情: